7 Zeitgleichung und Sunalmanac - Postmoderne Astronavigation

Inhaltsverzeichnis

Links → Kapitel 1, Kapitel 2, Kapitel 3, Kapitel 4, Kapitel 5 und 6, Kapitel 8

Mit dem Stand der Sonne kann nur dann navigiert werden, wenn dafür auch die wahre Sonnenzeit genutzt wird. Diese weicht jedoch von der Zeitangabe uns bekannter Uhren, wie Schiffschronometer, Quarzuhr oder Atomuhr, man bezeichnet diese Instrumente wegen ihres gleichmäßigen Laufs auch als Räderuhren, erheblich ab. Die von Räderuhren angegebene Zeit läuft absolut gleichmäßig, die Erde bewegt sich aber von der Sonne aus gesehen nicht gleichmäßig. Sie bewegt sich mit unterschiedlicher Geschwindigkeit auf einer elliptischen Bahn und ihre Erdachse scheint dabei zu taumeln, was zur Folge hat, dass die Tageslängen zwischen zwei Mittags-Höchstständen der Sonne am selben Ort unterschiedlich lang sind – geringfügig zwar, aber es summiert sich. Die von gleichmäßig laufenden Uhren angezeigte Zeit ist deshalb im Vergleich mit der wahren Sonnenzeit eine mittlere Zeit, weil sich alle Unregelmäßigkeiten im Verlauf eines Jahres wieder ausgleichen. Die wahre Sonnenzeit wird von Sonnenuhren angezeigt und es ist bekannt, dass ihre Zeitangaben von denen einer normalen Quarz-Armbanduhr im Laufe eines Jahres um eine Viertelstunde vor- oder nachgehen kann.

Weil die Navigatoren für ihre Arbeit nur die von einem Schiffschronometer angezeigte Zeit zur Verfügung hatten, brauchten sie Angaben über eine Zeitkorrektur, die mit der Chronometerzeit addiert die wahre Sonnenzeit liefert. Diese Korrekturzeit oder besser Ausgleichszeit ist die Zeitgleichung. Es handelt sich dabei nicht um eine Gleichung im mathematischen Sinn. Vielmehr ist es der Verlauf einer Zeitfunktion über einen Zeitraum, beispielsweise von einem Jahr, die zum Ausgleich der mittleren Zeitangabe einer Räderuhr notwendig ist, um daraus die wahre Sonnenzeit zu erhalten. Eine praktische Anwendungsform ist eine Tabelle mit Zeitangaben für jeden Tag um 12:00 UT1 eines Jahres. Der Begriff Zeitgleichung ist also von ihrer Funktion des Ausgleichens abgeleitet.

In unserem normalen Leben gestaltet sich dies umgekehrt. Dort bestimmt die mittlere Zeit unseren Tagesablauf. Wer zehn Minuten zu spät kommt, kann sich nicht damit rechtfertigen, dass er den Termin nach der wahren Sonnenzeit wahrnehmen wollte. Es ist nämlich sehr lange her, dass Menschen ihren Tagesablauf vom Lauf der Sonne abhängig gemacht haben. Heute künden nur noch einige Sonnenuhren davon. Die Existenz einer Zeitgleichung wurde schon in der Antike vermutet. Doch erst nach Bekanntwerden der Keplerschen Gesetze wurde sie greifbar und 1672 von John Flamsteed (1646–1719) erstmals berechnet. Die Geheimnisse dieses Naturereignisses, das allgemein nur wenig bekannt ist, für die Navigation mit der Sonne jedoch die wichtigste Grundvoraussetzung darstellt, sollen deshalb nachfolgend genauer untersucht werden.

7.1 Elliptizität der Erdbahn

Die Zeitgleichung beruht auf zwei unabhängigen Ursachen. Die erste davon ist die elliptische Umlaufbahn der Erde um die Sonne. Gemäß dem ersten Keplerschen Gesetz umkreist die Erde die Sonne auf einer elliptischen Bahn, wobei sich die Sonne in einem Brennpunkt dieser Ellipse befindet. Die Form der Ellipse weicht nicht wesentlich von einem Kreis ab, denn ihre numerische Exzentrizität ist mit 0,0167 recht gering. In einer maßstabgerechten Zeichnung könnte man die tatsächlich elliptische Umlaufbahn optisch von einem Kreis gar nicht unterscheiden. Die Darstellung im Bild 7.1 ist deshalb stark übertrieben.

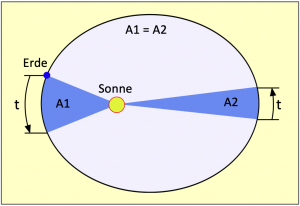
**Bild 7.1: Grafik zum 1. und 2. Keplerschen Gesetz.**

Im Nordwinter kommt die Erde der Sonne am nächsten. Dann erscheint ihre Scheibe auch ein klein wenig größer. Im Sommer hat sie zur Sonne den größten Abstand. Der kleinste und der größte Abstand zur Sonne sind der Perihel und der Aphel, sie bilden die Enden der Hauptachse der Ellipse. Sie stimmen jedoch nicht exakt mit den Sonnenwenden überein. An den Sonnenwenden hat die Sonne ihre größte nördliche bzw. größte südliche Höhe über dem Horizont. Der Perihel wird gegenwärtig am 2. Januar erreicht, während die Sonne ihren niedrigsten Stand auf der Nordhalbkugel bereits am 21. Dezember, also einige Tage davor hat. Der Perihel ändert sich in 60 Jahren um etwa einen Tag.

Am Perihel ist die Massenanziehung zwischen Erde und Sonne am größten. Damit die Erde dadurch nicht in die Sonne stürzt, erhöht sie zum Ausgleich der zunehmenden Gravitationskraft ihre Bahngeschwindigkeit und damit ihre Fliehkraft. Dies hat Kepler in seinem zweiten Gesetz exakt beschrieben:

„Ein von der Sonne zum Planeten gezogener Fahrstrahl überstreicht in gleichen Zeiten gleich große Flächen.“

Bild 7.1 zeigt das schematisch. Die Flächen A1 und A2 sind gleich groß und werden von einem Fahrstrahl zwischen Erde und Sonne in einem gleich großen Zeitintervall t überstrichen. Die Bahngeschwindigkeit der Erde ist bei dieser Betrachtung logischerweise dann am größten, wenn in der Zeit t die längere Strecke zurückgelegt wird.
Die unterschiedlichen Bahngeschwindigkeiten wirken sich auf die Zeitgleichung aus. Die Erde dreht sich sehr gleichmäßig und eine Drehung der Erde von 360° um sich selbst dauert 23 Stunden, 56 Minuten und 4,0905 Sekunden. Diese Zeit ist ein Sterntag, weil sich auf einem Meridian nach jeweils einem Sterntag immer wieder derselbe Sternenhimmel ausbreitet. Während sich die Erde dreht, kommt sie gleichzeitig auf ihrer Bahn um die Sonne ein Stück weiter – und das hat besondere Auswirkungen.
Bild 7.2 zeigt die Erde in der Position 1, wo die Sonne auf einem ihr gerade zugewandten Meridian kulminiert. Nach mehreren vollen Erdumdrehungen von jeweils 360° befindet sich die Erde in Position 2 und derselbe Meridian, der sich in Position 1 noch der Mitte der Sonne zuwandte, zeigt jetzt an der Sonne vorbei auf die Himmelskugel mit den Fixsternen. Damit derselbe Meridian an einem jeweils folgenden Tag immer wieder genau auf die Mitte der Sonnenscheibe zeigt, muss sich die Erde täglich etwa vier Minuten weiterdrehen und dadurch kommen wir auf 24 Stunden, die ein Sonnentag dauert.

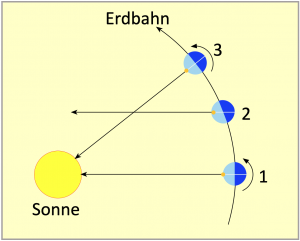
**Bild 7.2: Die Erde muss nach jeder Umdrehung um sich selbst noch etwa 4 Minuten nachdrehen, bis eine Kulmination der Sonne erfolgen kann.**

Wenn täglich immer nur genau vier Minuten zum Sterntag addiert werden, damit die Sonne auf demselben Meridian kulminiert, erklärt das noch keinen Zeitunterschied zwischen Räderuhr und Sonnenzeit. Das wäre bei einer exakt kreisförmigen Erdumlaufbahn der Fall. Deshalb sollte sich auch am Bild 7.1 orientiert werden. In Sonnennähe bewegt sich die Erde auf ihrer Bahn schneller und das bedeutet, sie kommt innerhalb einer Tagesetappe ein Stück weiter voran als in Sonnenferne. Sie lässt dadurch die Sonne auf ihrer Bahn jeden Tag etwas weiter zurück und muss darum auch jeden Tag etwas länger als vier Minuten nachdrehen. In Richtung Sommer auf der Nordhalbkugel entfernt sich die Erde wieder von der Sonne und ihre Bahngeschwindigkeit nimmt ab. Sie legt jetzt auf ihrer Bahn in jeder Tagesetappe etwas kürzere Stücke zurück. Dadurch lässt sie die Sonne nach jeder Eigendrehung nicht mehr so weit hinter sich. Dafür muss sie jetzt auch weniger nachdrehen und ihre Nachdrehzeiten werden kleiner als vier Minuten.
Die daraus resultierende Änderung der wahren Tageslänge zwischen zwei Tagen beträgt maximal etwa ±8 Sekunden. Da sich die Zeiten summieren, ergibt sich innerhalb eines Jahres eine maximale Schwankung der wahren Sonnenzeit um etwa ±7,5 Minuten in einem angenähert sinusförmigen Verlauf.

7.2 Schiefe der Ekliptik

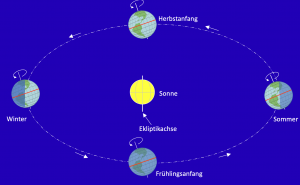
Eine zweite Ursache des Unterschiedes von Sonnenzeit und Chronometerzeit ist die Schiefe der Ekliptik. Die Erdachse steht etwa 23,44° schräg zur Ebene der Ekliptik und damit auch zur Achse der Ekliptik. Diese Stellung ist in Bezug zum Fixsternhimmel nahezu unveränderlich. Von der Sonne aus gesehen scheint die Erdachse jedoch zu taumeln. An den Tagundnachtgleichen steht sie von der Sonne aus gesehen einmal mit +23,44° und einmal mit -23,44° maximal schräg zur Ekliptikachse. In den Sonnenwenden steht sie zwar immer noch schräg zur Ekliptikebene, doch von der Sonne aus gesehen sind beide Achsen deckungsgleich hintereinander angeordnet. Dafür ist die Nord- oder die Südhalbkugel der Sonne zugeneigt und wird jeweils direkter angestrahlt, woraus sich die Jahreszeiten ergeben.

**Bild 7.3: Die Erde auf ihrer Bahn um die Sonne**

Um den Einfluss der Schiefe der Ekliptik auf die Zeitgleichung zu erfassen, müssen mindestens die folgenden drei Bewegungen berücksichtigt werden:

- Erdrotation:  0,25°/min oder  15,00 NM/min am Äquator
- Bahngeschwindigkeit v:   v = 0,986°/d oder 59,14 NM/d
- Deklination δ:  δ = 0° bis 23,44°  vom 20. März bis 21. Juni

An dieser Stelle soll noch einmal an den Bildpunkt oder Zenitalpunkt eines Gestirns erinnert werden. Der Bildpunkt der Sonne ist der Ort, an dem eine gedachte Linie zwischen dem Mittelpunkt der Sonne und dem Mittelpunkt der Erde die Erdoberfläche durchbricht. Es ist der Ort, an dem ein Beobachter die Sonne im Zenit sieht.
Die Erde muss nach jeder Umdrehung um sich selbst, also nach einem Sterntag, im Mittel noch etwa vier Minuten nachdrehen, damit die Sonne auf demselben Meridian des Vortages kulminiert. Dieser Kulminationsmeridian befindet sich nach jeder Drehung der Erde um sich selbst und noch vor Beginn der Nachdrehung ein Stück weit westlich vom Bildpunkt. Gleichzeitig ist die Erde während ihrer Rotation auch eine Tagesetappe auf der Umlaufbahn weitergekommen, wie dies im Bild 7.4 zu sehen ist. Dieses Stück lässt sich ausrechnen. Aus dem Produkt der Bahngeschwindigkeit von 0,986°/d und der Rotationsgeschwindigkeit von 60 NM/Grad erhält man

$s=\frac{0,986\,\text{Grad}}{d}\cdot\frac{60 \,\text{NM}}{\text{Grad}}=\frac{59,14\,\text{NM}}{d}\cdot$

Diese Strecke liegt immer in der Ebene der Ekliptik bzw. senkrecht zur Achse der Ekliptik. Daraus lassen sich jetzt zwei Extreme ableiten, die im Bild 7.4 links und rechts gezeigt werden.

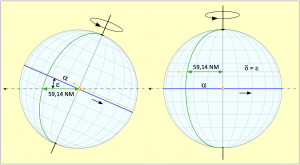
Bild 7.4: Die Erde legt auf ihrer Umlaufbahn täglich 59,15 NM zurück. Der Kulminationsmeridian vom Vortag (grün) erreicht eine Folgekulmination an den Tagundnachtgleichen (links) eher als an den Sonnenwenden (rechts).

Der Vorgang ist Folgender: An den Tagundnachtgleichen, links im Bild, trifft der Bildpunkt der Sonne den Äquator. Mit fortschreitendem Weg auf der Umlaufbahn neigt sich eine der Erdhalbkugeln der Sonne zu und der Bildpunkt weicht nach Norden oder Süden aus. Infolge der Erdrotation legt er dabei auf der Erdoberfläche eine Spiralbahn mit immer enger zusammenliegenden Windungen zurück. Im Bild ist der Beginn der Spiralbahn in gelb angedeutet, weil sich der Nordpol in dem Beispiel der Sonne zuneigt. Beim Erreichen der Sommersonnenwende wird eine Bahn entlang des Wendekreises und parallel zum Äquator gezeichnet. Von der Sonne aus gesehen hat sich in diesem Vierteljahr die Erdachse völlig aufgerichtet, wie das Bild auf seiner rechten Seite zeigt.
Jetzt gehen wir wieder zurück an den Frühlingsanfang und damit auf die linke Bildhälfte. Dort bilden der grün dargestellte Kulminationsmeridian vom Vortag, der Äquatorabschnitt mit der Länge α und die Tagesetappe von s = 59,14 NM, die hier mit einer Bildpunktspur von 0,986° auf einem Großkreis gleichkommt, ein rechtwinkliges Kugeldreieck, wobei der rechte Winkel zwischen Meridian und Äquator existiert. In dem Dreieck ist die Strecke s die Hypotenuse und somit die längste Seite. Der Winkel ε existiert zwischen der Ebene der Ekliptik und dem Äquator. Daraus kann jetzt die Strecke α berechnet werden. Diese Strecke muss die Erde auf ihrer Achse noch nachdrehen, damit die Sonne auf dem grün gezeichneten Meridian kulminieren kann. Die Formel zur Berechnung von α lautet:

$\alpha=\arctan(\tan s\cdot\cos \epsilon)$

Nach dem Einsetzen der Zahlen mit s = 0,986° und ε = 23,44° errechnet sich daraus ein Winkel α von 0,904°. Mit ihrer Rotationsgeschwindigkeit von 15°/h benötigt die Erde dafür genau 3,618 Minuten Nachdrehzeit, bis der grün gezeichnete Meridian durch Erdrotation den Bildpunkt bzw. Kulminationspunkt erreicht. Die Differenz zu der mittleren täglichen Nachdrehzeit von 3,943 Minuten beträgt hier -19,51 Sekunden. Damit ist ein Sonnentag am Frühlingsanfang und ebenso am Herbstanfang kürzer als ein mittlerer Sonnentag.
In den Wendepunkten ist die Nord- oder Südhalbkugel der Sonne zugeneigt und der Bildpunkt der Sonne schreibt seine Spur infolge der Erdrotation auf einem Wendekreis, mit der Breite $\varphi$ ≈ 23,44°, die in diesem Zeitpunkt die Größe von plus oder minus ε besitzen wird. Dort liegen die Meridiane dichter zusammen und die während einer Tagesetappe auf der Umlaufbahn gezeichnete Bildpunktspur von 59,14 NM Länge kann einen größeren Winkel bzw. einen größeren Meridianbereich überstreichen. Dieser Winkel ist gleich dem Winkel α auf dem Äquator, nur hat er dort eine größere Länge in nautischen Meilen, die ein längeres Nachdrehen erfordert. Der Winkel besitzt die Größe von

$\alpha=\frac{s}{\cos\epsilon}\cdot$

Das ergibt nach dem Einsetzen der Zahlen einen Wert von 1,075°, wozu die Erde 4,299 Minuten nachdrehen muss. Das sind dann 21,32 s mehr als die mittlere Rotationszeit und damit ist der Sonnentag an den Sonnenwenden um diese Zeit länger als die mittlere Sonnenzeit.
Vom Frühlingsanfang beginnend addieren sich die täglichen Sekunden etwa 46 Tage lang bis auf etwa 9,85 Minuten. Diese Summe nimmt dann in den weiteren 46 Tagen bis zur Sommersonnenwende wieder bis auf 0 ab. Weil das Auf und Ab zweimal im Jahr geschieht, ergeben sich über das ganze Jahr gesehen zwei komplette sinusähnliche Wellen der Zeitverschiebung.

7.3 Berechnungsmodell

Für eine genauere und umfassendere Berechnung muss auf das Kepler-Modell zurückgegriffen werden. Das ist ein Zweimassenmodell, das nur die Massen von Erde und Sonne berücksichtigt und die Massen von Mond und den großen Planeten vernachlässigt. Dadurch entstehende Abweichungen sind jedoch nicht erheblich. In einer Längenberechnung würden sie Fehler von bis zu etwa $\pm$ 0,5’ verursachen und spielen deshalb in einer praktischen Navigation keine allzu große Rolle. Fehler in der Messung von Zeit und Höhe bewirken größere Abweichungen. Bild 7.5 zeigt das zur Berechnung geeignete Modell einer geozentrischen Darstellung, des Systems Erde-Sonne wie man es von der Erde aus wahrnimmt.
Letztendlich ist es egal, von welcher Warte aus die Gesetzmäßigkeiten betrachtet werden. Sie sind immer gleich. Lediglich hinsichtlich der Anschauung ist es günstig, die Warte zu wechseln und mal ein geozentrisches wie im Bild 7.5 und ein anderes Mal ein heliozentrisches Modell wie Bild 7.3 zu betrachten. Das Modell zeigt die Himmelskugel mit der rotierenden Erde im Mittelpunkt. Die Sonne S umrundet die Erde einmal im Jahr auf ihrer ekliptischen Bahn, die zum Himmelsäquator und auch zum Erdäquator die gleiche Schräge von ε besitzt, mit einer völlig gleichmäßigen Geschwindigkeit.

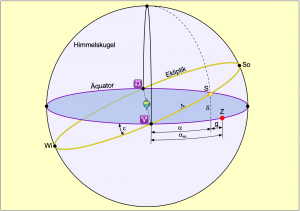
**Bild 7.5: Die Erde im Zentrum der Himmelkugel.**

Vom Frühlingspunkt ausgehend, das ist einer der beiden Schnittpunkte von Himmelsäquator und Ekliptik an der Himmelskugel, bewegt sich die Sonne nordwärts und bescheint die Nordhalbkugel der Erde zunehmend direkter. Dabei erreicht sie als nördlichsten Punkt die Sommersonnenwende So und bewegt sich danach auf ihrer Bahn wieder südwärts.
Genau am Herbstanfang, dem zweiten Schnittpunkt von Äquatorebene und Ebene der Ekliptik, passiert der Bildpunkt den Äquator und bewegt sich dann weiter südwärts, wobei die Sonne die Südhalbkugel direkter bestrahlt. Schließlich passiert die Sonne die Wintersonnenwende Wi und erreicht zum Abschluss der Umrundung wieder den Frühlingspunkt.

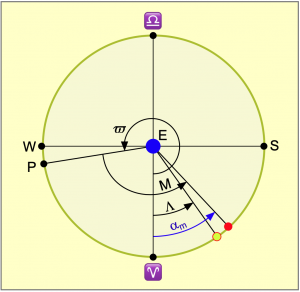
Auf dem Himmelsäquator soll eine Vergleichssonne Z analog dem Zeiger einer großen Uhr kreisen und zwar mit derselben gleichmäßigen Bahngeschwindigkeit wie die richtige Sonne. Außerdem passieren beide Sonnen den Frühlingsanfang und den Herbstanfang zum selben Zeitpunkt. Der jeweilige Meridian der Himmelskugel, der durch die echte Sonne verläuft, trifft den Himmelsäquator im rechten Winkel, wobei dieser Schnittpunkt die Länge α_m in die Abschnitte α und g teilt. Unter der Länge von g ist die Zeitgleichung zu verstehen.
Es gibt jedoch ein Problem. Jedes Mal, wenn die Sonne nach einem kompletten Umlauf wieder den Frühlingspunkt erreicht, trifft ihr Bildpunkt einen anderen Meridian auf der Erde.
So gibt es keine Anzahl von 360° Erdrotationen, die ohne Rest auf einen Umlauf passen, zumal die Erde immer langsamer dreht. So beginnt jedes Jahr am 1. Januar 00:00:00 UT auf einem anderen Meridian.
Genau deshalb braucht man für jedes Jahr eine neue Tabelle mit der Zeitgleichung oder einen Almanach, der genau nur für ein bestimmtes Jahr gilt. Da muss man fragen, wann die Erde angefangen hat, sich zu drehen, natürlich nur im kalendarischen Sinne. Die Antwort lautet: am 1.1.4713 v. Chr., also vor beinahe 7000 Jahren. So lange kennt man also schon Kalender, in denen die Tage bis heute fortgezählt werden. Allerdings gab es viele Kalenderreformen, in denen die Kalender an das Sonnenjahr angepasst wurden. Der römische Kaiser Gaius Julius Cäsar reformierte im Jahr 45 v. Chr. den bis dahin gültigen römischen Kalender. In diesem neuen von ihm geschaffenen julianischen Kalender hatte ein Jahr 365 Tage und jedes vierte Jahr war ein Schaltjahr mit 366 Tagen. Dieser Kalender hinkte alle 128 Jahre um einen Tag der auf dem Frühlingsanfang beruhenden astronomischen Realität hinterher. Dennoch wird er auch heute noch in einigen Ländern verwendet.
Im Jahr 1582 reformierte Papst Gregor den Kalender, indem zehn Tage einfach übersprungen wurden, denn das Osterdatum war nicht mehr durch den Frühlingsanfang und Frühlingsvollmond bestimmt. Auch die Schaltjahresregel wurde geändert, sodass zwar grundsätzlich alle vier Jahre ein Schalttag dazukommt, dieser jedoch in den Jahrhundertwenden ausfällt, es sei denn die Jahreszahl ist restlos durch 400 teilbar. Den gregorianischen Kalender haben inzwischen die meisten Staaten übernommen. Doch es bleibt dabei – es wird keinen Kalender geben können, in dem Sonnenjahr und Kalenderjahr übereinstimmen.
Damit nicht immer bis zu einem Tag in weiter Vergangenheit zurückgerechnet werden muss, wurden Etappen festgelegt. Die zuletzt zurückgelegte Etappe endete am 1. Januar 2000 um 12:00:00 UT1. Für dieses Referenzdatum wurden die aktuellen Werte der Bahnelemente der Erde als lineare Gleichungen abgelegt.
Die Gleichungen sind in der Tafel 7.1 angegeben. Sie besitzen alle die Form Y = A + B ⋅ T, sind also lineare Gleichungen ersten Grades, wobei A die Konstante des jeweiligen Parameters Y am Referenzdatum ist und das Produkt B ⋅ T die mit den zukünftigen Tagen T zu erwartenden Änderungen beschreibt.

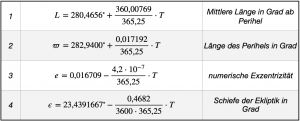
**Tafel 7.1: Bahnelemente des Planeten Erde.**

Die Tafel 7.1 enthält alle wichtigen zum Referenzdatum festgelegten Bahnelemente. Darin bedeuten:

1. Mittlere Länge in Grad ab Perihel ist die Stelle auf dem Himmelsäquator, die ein dort kreisender Punkt erreicht, wenn er gleichmäßig wie ein Uhrzeiger mit der mittleren Umlaufgeschwindigkeit der Sonne vom Referenzdatum an unterwegs ist. Innerhalb von 10 Jahren legt L dann eine Länge von rund 3600°zurück.
2. Länge des Perihel in Grad ist der Punkt auf der Erdumlaufbahn, an dem die Erde im Nordwinter der Sonne am nächsten kommt. Die Länge wird in Grad vom Frühlingspunkt aus gemessen.
3. Numerische Exzentrizität ist ein Parameter, mit dessen Hilfe ein Kreis in eine Ellipse verwandelt wird, in unserem Fall also ein mathematisches Hilfsmittel, mit dem die elliptische Bahn der Erde um die Sonne festgelegt wird.
4. Schiefe der Ekliptik in Grad ist der Winkel, den die Ebene der Ekliptik gegenüber der horizontalen Ebene einnimmt. Es ist gleichzeitig der Winkel der maximal möglichen Deklination der Sonne.

7.3.1 Bestimmung der Zeit als Variable

Für eine Navigation werden die Sonnenpositionen – Deklination δ als Abweichung vom Äquator und Stundenwinkel Grt als Längenabstand zu einem festgelegten Nullmeridian – gebraucht. Es sollte möglich sein, diese aus den Bahnelementen heraus berechnen zu können. Es muss gelingen, die Position der Sonne bzw. die Koordinaten ihres Bildpunktes auf der Erdoberfläche, was dasselbe ist, für eine beliebige Sekunde eines beliebigen Jahres im Voraus zu berechnen. Erst dadurch wird ein Navigator in die Lage versetzt, unter Zuhilfenahme einer sekundengenauen Feststellung der Sonnenhöhe über dem Horizont, die Koordinaten des Bildpunktes der Sonne ausrechnen zu können. Aus den Koordinaten von zwei zu verschiedenen Zeiten errechneten Bildpunkten in Bezug zum Erdpol und seiner noch unbekannten eigenen Position kann diese schließlich ermittelt werden.
Die vier Bahnelemente in Tafel 7.1 beschreiben also die Stellung der Sonne auf der Ekliptik in Bezug zur Erdstellung, als Funktion der Zeit T. Somit besteht die erste Aufgabe darin, diese Zeit in Tagen als Dezimalzahl mit entsprechend vielen Stellen nach dem Komma auszurechnen. Die Formel dafür lautet:

(7.1) $T=\mathbb{Z}\Bigr(\big(JJJJ-2000\big)\cdot 365,25\Bigr)+N-0,5+\frac{UT1}{24}-SJ\cdot$

Hierin gilt bis 2099 die Schaltjahresdefinition

(7.2) $SJ=\text{wenn}\;4|(JJJJ -2000)\;\text{dann}\;1\;\text{sonst}\;0\cdot$

Mit ℤ ist der ganzzahlige Teil des Wertes gemeint, der in der nachfolgenden Klammer steht. So liefert das Jahr 2022 in der großen Klammer den Wert 8035,5. Dann ist ℤ = 8035, weil der Nachkomma-Anteil von 0,5 einfach weggelassen wird. Die zu subtrahierende 2000 ist die Jahreszahl des Referenzdatums.
Mit N werden die im betrachteten Jahr vergangenen Tage einschließlich des aktuellen Tages bezeichnet. So beträgt N an einem 12. Februar 43 Tage. Die -0,5 Tage sind nötig, weil die Sonne auf dem Nullmeridian nicht um 0 Uhr, sondern Mittags kulminiert. Das ist eine willkürliche Festlegung, die auf der Tradition beruht, dass 12 Uhr die Mittagszeit ist und die Sonne am Mittag ihren höchsten Stand hat.
Der nachfolgende Bruch UT1/24 legt mit der Dezimalzahl von UT1 den gebrochenen Tagesanteil fest. Mit SJ ist die mit der Gleichung 7.2 beschriebene Schaltjahresregel gemeint, die in dieser vereinfachten Form bis 2099 gilt. Ein Schaltjahr gibt es danach immer dann, wenn die Jahreszahl ohne Rest durch vier teilbar ist. Gelesen wird diese Gleichung als:

Wenn 4 der Teiler von (JJJJ – 2000) ist, dann 1, wenn nicht, dann 0.

Somit ist jedes vierte Jahr ein Schaltjahr, in dem dann ein Tag abgezogen werden muss. Subtrahieren ist deshalb angesagt, weil bei der Multiplikation mit 365,25 der Nachkommawert von 0,25 alle vier Jahre einen zusätzlichen Tag hervorbringt. Das Jahr 2100 ist kein Schaltjahr, obwohl es durch 4 teilbar ist. Es ist aber auch durch 100 teilbar und fällt deshalb als Schaltjahr aus. Die Regelung mit der Gleichung 7.2 gilt daher nur bis ins Jahr 2099.
Zur Zeitmessung verwenden die Menschen mechanische Uhren, die sehr gleichmäßig laufen. Der von diesen Uhren angezeigte Lauf der Zeit ist mit dem Lauf der Vergleichssonne Z im Bild 7.5 vergleichbar, deren Bildpunkt den Äquator nie verlässt, aber pro Zeiteinheit immer die gleiche Längengraddifferenz zurücklegt. Das ist bei der echten Sonne nicht der Fall, denn bei ihr ist es pro Zeiteinheit immer eine andere Längengraddifferenz.
Nehmen wir ihre Geschwindigkeit auf der Umlaufbahn als konstant an, dann überschreitet ihr Bildpunkt in derselben Zeit mehr Meridiane, wenn ihr die Nord- oder Südhalbkugel zugewandt ist, als wenn ihr der Äquator zugewandt ist, wo die Meridiane am weitesten auseinanderliegen. Der Längengrad, auf dem sich der Bildpunkt der wahren Sonne gerade befindet, unterscheidet sich von dem Längengrad, auf dem sich der Bildpunkt der Vergleichssonne befindet, um den im Bild 7.5 gezeigten Betrag g. Dieser Längengrad-Unterschied ist die Zeitgleichung, weil 1° Längendifferenz dasselbe ist wie vier Minuten Sonnenlaufzeit. Wenn es also darum geht, die Bildpunktlänge der wahren Sonne mit der Zeitangabe einer Räderuhr festzustellen, dann ist deren Zeitangabe eine mittlere Zeit und die wahre Sonnenzeit erhält man erst durch die Addition der Zeitgleichung.

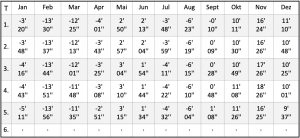
**Tafel 7.2: Ausschnitt aus einer Tabelle mit der Zeitgleichung des Jahres 2022 für 12:00 UT1**

Früheren Navigatoren stand für jedes Jahr die Zeitgleichung in Form einer Tabelle zur Verfügung, wie sie hier als Ausschnitt in der Tafel 7.2 gezeigt wird. Ein Navigator ermittelte den Stundenwinkel der Sonne nach der von einem Chronometer angezeigten Zeit, die er mit der Zeitgleichung korrigieren musste. War die Differenz des Korrekturbetrages von einem auf den anderen Tag zu groß, dann musste sie sogar auf die Stunde der Beobachtung umgerechnet werden. Später wurde der Aufwand dieser Umrechnung dadurch behoben, dass Tabellen herausgegeben wurden, in denen für jeden Tag der Stundenwinkel im Stundenraster angegeben wurde. Dies waren dann die Nautischen Jahrbücher.

7.3.2 Berechnung der Zeitgleichung

Nach Bild 7.5 ist die Zeitgleichung einfach die Auflösung der Beziehung

(7.3) $g=\alpha_m-\alpha\cdot$

Unter _αm versteht man den Hauptwinkel der Länge L. So hat die Erde beispielsweise Anfang Juli 2021 ihre Bahn um die Sonne schon etwa 21,5-mal mit je 360° ausgeführt und das wären dann knapp 21,5 ⋅ 360° = 7740° plus die 280° vom Frühlingspunkt bis zum Perihel. Insgesamt wären das dann 8020°. Die genaue Zahl liefert das Bahnelement L. Den Hauptwinkel erhält man dadurch, dass volle 360°-Umrundungen aus der Zahl herausgenommen werden. Dafür gilt dann die folgende Formel:

(7.4) $\alpha_m=L-\mathbb{Z}\Bigg(\frac{L}{360^\circ}\Bigg)\cdot 360^\circ\cdot$

Mit der Berechnung von α wird es dann schon komplizierter. Wie Bild 7.5 zeigt, bilden Λ, α und δ, alles sind Großkreisabschnitte, ein rechtwinkliges Kugeldreieck mit dem rechten Winkel zwischen α und dem durch die Sonne gehenden Meridian. Für dieses Dreieck ist die Berechnungsformel in einem Formelbuch mit tan α = tan Λ ･ cos ε schnell gefunden.
Unter Berücksichtigung der Vollkreisigkeit ist es jedoch günstiger, mit der Transformationsformel

(7.5) $\begin{equation*}\alpha=\arctan_\Lambda(\tan\Lambda\cdot\cos\epsilon)\end{equation*}$

zu arbeiten. Man wäre sonst mit zu vielen Überläufen konfrontiert. Der Index Λ in der Arkusfunktion ruft den Winkel auf, der Λ am nächsten liegt. Diese Formel ist dann folgendermaßen zu verwenden:

(7.6) $\alpha=\arctan_\Lambda(x)=\arctan(x)+\pi\cdot \mathbb{Z}\Bigg(\frac{\Lambda-\arctan(x)}{\pi}\Bigg)\cdot$

Hierin bedeutet $x =\tan\Lambda\cdot\cos\epsilon$ . Um die Gleichung lösen zu können, wird Λ gebraucht und dafür gilt:

(7.7) $\begin{equation*}\Lambda=\alpha_m+C \cdot\end{equation*}$

Mit C kommt hier die sogenannte Mittelpunktsgleichung ins Spiel, die zur Berechnung einer elliptischen Bahn durch elliptische Verformung einer Kreisbahn dient. Sie hängt nach Kepler von der Exzentrizität e der jeweiligen Bahnellipse ab und ist die Differenz zwischen mittlerer Anomalie M und wahrer Anomalie V. Das soll an dieser Stelle allerdings nicht weiter vertieft werden. Die mittlere Anomalie ist die Differenz aus mittlerer Länge und Länge des Perihels. Dafür gilt:

(7.8) $\begin{equation*}M=\alpha_m-\varpi+360^\circ\cdot\end{equation*}$

Der zusätzliche Vollkreiswinkel von 360° in dieser Gleichung spielt keine Rolle, da im Weiteren nur der Sinus von M benutzt wird. Es ist dann völlig gleich, wie oft 360° dazu addiert werden. Auch die Formel M = L – $\varpi$ würde dasselbe Ergebnis liefern, das nur grafisch nicht so einfach wiedergegeben werden könnte.
Da die Kepler-Gleichung nur iterativ zu lösen ist und die Exzentrizität der Erdbahn mit e = 0,0168 recht klein ausfällt, ist hier eine Reihenentwicklung sinnvoller. In der Literatur findet man dafür:

$C=\frac{180}{\pi}\Bigg((2e-\frac{e^3}{4})\cdot\sin M+\frac{5}{4}e^2\cdot\sin (2M)+\frac{13}{12}e^3\cdot\sin (3M)+$

(7.9) $+\frac{103}{96}e^4\cdot\sin 4M+\frac{1097}{960}e^5\cdot\sin (5M)\Bigg)\cdot$

Die dritte Zeile dieser Gleichung bzw. die letzten beiden Summen in der Klammer können auch weggelassen werden. Sie bringen keinen nennenswerten Beitrag mehr zum Ergebnis. Mit dem Resultat kann jetzt Λ nach Gleichung 7.7 berechnet werden und liefert nach Ausrechnen der Gleichung 7.5 unter Benutzung der Lösungshilfe in Gleichung 7.6 die Länge α Damit lässt sich dann mit Gleichung 7.3 die Zeitgleichung in Grad angeben. Eine Multiplikation mit vier liefert das Ergebnis auch in Zeitminuten, wie sie z. B. in der Tafel 7.2 angegeben werden.
Die Zeitgleichung ist wie bereits beschrieben von der Exzentrizität und von der Ekliptikschiefe, also von zwei Komponenten abhängig. Der Beitrag aus der Bahnexzentrizität wird dadurch berechnet, dass Ekliptikachse und Erdachse parallel gestellt werden. Dafür gilt:

(7.10) $g_{\epsilon=0}=\alpha_m-\Lambda\cdot$

Dieser Teil verläuft sinusähnlich mit einer Periode in einem Jahr. Es ist die grüne Strich-Punkt-Kurve im Bild 7.7 und ergibt sich ebenfalls aus der Gl. 7.8 durch Umstellung auf -C = α_m – Δ als -C .
Die zweite Komponente ist der Beitrag, der auf die Schiefe der Ekliptik zurückzuführen ist und ergibt sich als

(7.11) $g_\epsilon=\Lambda-\alpha\cdot$

Die Anwendung des Arkustangens mit Lageparameter gemäß Gleichung 7.6 verhindert nicht, dass hier Zahlenwerte auftreten, die über die Erwartungen hinausgehen. Erwartet werden jedoch Werte, die über 0,07 – das entspricht 4° – keinesfalls hinausgehen. Sollten Zahlen errechnet werden, die über dieses Maximum hinausgehen, dann muss vom Ergebnis der Gleichung $\pi$ subtrahiert werden. Der Verlauf ist, wie oben bereits erwähnt, ebenfalls sinusförmig, jedoch mit zwei Perioden in einem Jahr. Dies ist im Bild 7.7 als rot gestrichelte Kurve dargestellt.

**Bild 7.7: Zeitgleichung für das Jahr 2023 schwarz, Wirkung der Exzentrizität grün, Wirkung der Ekliptikschiefe rot.**

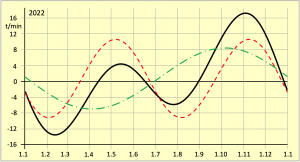
Die Zeitgleichung ist die Summe der mit den Gleichungen 7.10 und 7.11 beschriebenen Komponenten und somit

(7.12) $g=g_{\epsilon=0}+g_\epsilon=\alpha_m-\alpha\cdot$

Das Ergebnis ist, wie zu erwarten, die Gl. 7.3 und im Bild 7.7 als durchgehend schwarze Kurve gezeichnet.
Wenn die Zeitgleichungskomponenten nicht einzeln berechnet werden sollen, sondern die Zeitgleichung komplett und direkt, was für eine praktische Verwendung ausreicht, dann hilft die nachfolgend beschriebene Umformung. Durch Ersetzen von α in Gl. 7.12 bzw. 7.3 durch Gl. 7.5 kann die Zeitgleichung auch ausführlicher angegeben werden:

$g=\alpha_m-\arctan_\Lambda(\tan\Lambda\cdot\cos\epsilon)\cdot$

Ein Tangens Additionstheorem lautet:

$\tan(x-y)=\frac{\tan x-\tan y}{1+\tan x\cdot\tan y}$

Die Tangens-Umkehrfunktion liefert dafür:

$x-y=\arctan\frac{\tan x-\tan y}{1+\tan x\cdot\tan y}$

Mit x = ????_m und  $y=\arctan_\Lambda(\tan\Lambda\cdot\cos\epsilon)$ folgt daraus:

(7.13) $g=\arctan\frac{\tan \alpha_m-\tan \Lambda\cdot\cos \epsilon}{1+\tan \alpha_m\cdot\tan \Lambda\cdot\cos \epsilon}\cdot$

Alle bisher angegebenen Gleichungen liefern Winkeldaten und diese sogar fast immer im Bogenmaß, als Radiant. Die entsprechenden Zeitangaben erhält man daraus nach Multiplikation mit 4 Min/Grad.
Bild 7.7 zeigt die Verläufe der Zeitgleichung ab dem 1. Januar des Jahres 2022. Die beiden Komponenten sind farbig dargestellt. Die grün unterbrochene Linie entsteht aufgrund der Elliptizität der Erdumlaufbahn gemäß der Gleichung 7.10 und die rot unterbrochene Linie ist die Folge der Schiefe der Ekliptik gemäß der Gleichung 7.11. Durch die Addition der Funktionswerte erhält man die zusammengefasste Zeitgleichung, die als schwarze Kurve gemäß den Gleichungen 7.12 und 7.13 dargestellt ist.
An den vier Nulldurchgängen dieser Kurve ist zu sehen, dass die wahre Sonnenzeit nur an vier Tagen im Jahr mit der Zeit einer Räderuhr übereinstimmt und sonst bis zu einer Viertelstunde vor- oder nachlaufen kann. Die Kenntnis der Zeitgleichung ist unverzichtbar für eine Standortbestimmung mit der Sonne auf See.

7.4 Die Ephemeriden der Sonne

Darunter versteht man die Position der Sonne auf der Himmelskugel bzw. ihres Bildpunktes auf der Erde. Diese Position ist mit einer Längenkomponente, dem Greenwichwinkel und einer Breitenkomponente, der Deklination, beschrieben.
Die Einteilung des Gradnetzes der Erde in 180 positive Ostgrade und 180 negative Westgrade war im Sinne einer Navigation nicht optimal, weil sie nicht zum Lauf der Sonne passt. Der Stundenwinkel würde von 180° E zunächst bis auf null Grad am Nullmeridian herunterzählen und dann weiter ins Negative bis 180° bzw. -180° W. Man brauchte einen Stundenwinkel, der vom Nullmeridian ausgehend von 0° bis 360° mit dem Lauf der Sonne nach Westen aufwärts zählend einmal um die Erde geht. Parallel dazu sollte eine Uhr ihre 24 Stunden abdrehen.
Der Nullmeridian wurde 1884 auf der Meridiankonferenz in Chicago als derjenige festgelegt, der durch die Sternwarte von Greenwich geht. Der davon in Richtung Westen fortschreitende Stundenwinkel wurde – wie bereits erwähnt – Greenwich Hour Angle oder abgekürzt GHA genannt. Im deutschen heißt er Grt, was einfach Greenwichwinkel bedeutet.
Leider konnte die Uhrzeit nicht so angepasst werden, dass es immer 00:00 Uhr ist, wenn die Sonne am Nullmeridian startet. Ihr Start musste mit einem eindeutig zu definierenden Ereignis in ihrem Lauf beginnen und das ist nur die Kulmination. Die Sonne kulminiert aber mittags und Mittag ist es nach bürgerlicher Zeitauffassung um 12:00 Uhr. Um allem gerecht zu werden, wurde der Start der Sonne am Nullmeridian am Mittag festgelegt. Aufgrund der Zeitgleichung geschieht es jedoch nur viermal im Jahr , dass die Sonne den Nullmeridian um genau 12:00 Uhr bürgerlicher Zeit passiert.
Eine Navigation mit der Sonne funktioniert nur mit der wahren Sonnenzeit, die durch Addition von Chronometerzeit und Zeitgleichung erhalten wird. Die weitere Rechnerei umfasste zwar nur die Grundrechenarten, konnte jedoch auch mühselig werden. So gibt die Tafel 7.2 für den 4. Nov eine Abweichung von 18’ und 26’’an. Das sind dann pro Stunde etwa 0,75 Minuten Änderung, was bereits recht erhebliche Auswirkungen hat. Diese Umrechnung der Zeitgleichung auf die Tagesstunde wurde mit der Schaffung des Sonnenalmanachs überwunden.

7.4.1 Greenwichwinkel Grt

Um für die Zeit einer Sonnenbeobachtung den Greenwichwinkel zu erhalten, müssen von der Summe aus Chronometerzeit und Zeitgleichung 12 Sunden subtrahiert und das Ergebnis mit der Bildpunktgeschwindigkeit von 15°/h multipliziert werden.
Eine andere Möglichkeit besteht darin, primär nicht die Zeiten, sondern diese gleich als Stundenwinkel in Grad zu betrachten, wobei dann vier Minuten gleich ein Grad sind. Die Ordinate der Zeitgleichung im Bild 7.7 wäre dann nicht in $\pm$ 16 min skaliert, sondern in $\pm$ 4°. Dasselbe wird dann auch mit der Chronometerzeit gemacht, also ab 12:00 sind alle 4 min gleich 1 Grad. Dadurch erhält jede volle Stunde nach 12:00 einen formalen Stundenwinkel-Zuwachs um 15°.

**Tafel 7.3: Ausschnitt aus einem Sun Almanac vom 20. Aug. 2022**

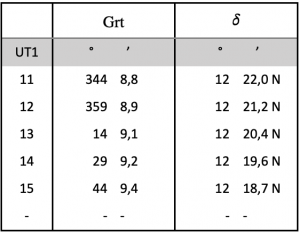
Wird jetzt – in einer Tabelle – jedem dieser gleichmäßig laufenden vollen Stundenwinkel die in Grad verwandelte Zeitgleichung zugeschlagen, dann entsteht daraus ein Sonnenalmanach. Der Vorteil ist weniger Rechenarbeit, dafür aber mehr Sucherei in einem neuen Tabellenwerk, das nämlich für jeden Tag eines Jahres eine extra Tabelle haben muss. Die Tafel 7.3 zeigt ihren prinzipiellen Aufbau mit Zahlen vom 20. August 2022.

Die erste Spalte enthält die Universalzeit UT1. Diese ist der Erdrotation angepasst und ist Referenzzeit für die völlig gleichmäßig laufende UTC oder Atomuhrzeit, die an Bord mit der Chronometerzeit gleichgesetzt wird. Da sich die Erde immer langsamer dreht, muss die UTC alle Jahre der UT1 angepasst werden. In der zweiten Spalte steht dann der Grt in Grad und Minuten. Man kann also auf diese Weise ohne vorherige Umrechnung der Chronometerzeit gleich den Grt bekommen. Für die Minuten und Sekunden einer Beobachtungsstunde muss interpoliert werden, was mithilfe von Schalttafeln am Ende des Almanachs möglich ist.
Der Greenwichwinkel startet auf diese Weise am Nullmeridian und zählt 360° rund um den Erdball. Da der Tag bei 180° E beginnt, der Nullmeridian aber 180° weiter westwärts liegt, muss dieser Versatz mit 12h berücksichtigt werden. Der Grt wird mit folgender Formel berechnet:

$Grt=g+15\cdot\big(t+12^h\big),$

(7.14) $Grt=g+15\cdot\big(t+12^h\big)\cdot$

Hierin ist t die Zeit UT1 des Tages im 24-Stunden-Lauf, für die der Grt berechnet werden soll. Die Zeit 12h ist die Zeit, die von der Sonne gebraucht wird, um von 180° E bis zum Nullmeridian zu kommen.
Der Ausdruck darunter besagt, dass der Klammerinhalt nicht größer als 24h sein darf. Für Nachmittags-Zeiten müssen deshalb immer 24 Stunden subtrahiert werden. Mit 15 ist die Winkelgeschwindigkeit der Sonne von 15°/h gemeint und g ist die in Grad angegebene Zeitgleichung gemäß Gleichung 7.13.

7.4.2 Deklination δ

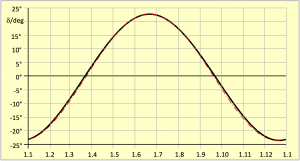
Die ersten Deklinationstabellen gab es schon im Mittelalter. Man stellte sie sich als Sinuswelle vor, die an den Tagundnachtgleichen einen Nulldurchgang hatte und an den Sonnenwenden ihre jeweiligen Maximalwerte von 23,44° erreichte. Das kam auch ungefähr hin, wie Bild 7.8 zeigt. Tatsächlich ist es aber eine Näherung, weil diese Annahme die Wirkung der Zeitgleichung ignoriert. Die Deklination kann leicht genau ausgerechnet werden. Im Bild 7.5 ist leicht erkennbar, dass es sich bei dem Dreieck mit den Seiten δ, Λ und α um ein rechtwinkliges Dreieck handelt. Der rechte Winkel existiert dabei zwischen den Seiten α und δ und die Seite δ kann deshalb mit einer einfachen Formel aus dem Formelbuch leicht ausgerechnet werden. Durch das Einsetzen der entsprechenden Größen erhält man:

(7.15) $\delta=\arcsin(\sin\epsilon\cdot\sin\Lambda)\cdot$

Die Länge Λ liefert die Gleichung 7.7. Durch Multiplikation mit dem Quotienten 180°/ $\pi$ wird der Winkel in Grad erhalten. Einen kleinen Ausschnitt der Deklinationen am 20. August 2022 zeigt Tafel 7.3 ebenfalls in der rechten Spalte.

**Bild 7.8: Deklination im Jahr 2023 schwarz. Die rote Strichpunktkurve markiert einen reinen sinusförmigen Verlauf.**

7.4.3 Das Nautische Jahrbuch

Ein Nautisches Jahrbuch ist allerdings sehr viel umfangreicher angelegt. Es besitzt für jeden Tag des Jahres eine sog. Tagseite. Darauf werden die Gestirnspositionen als Greenwich Stundenwinkel Grt, die Deklination δ im Stundenraster für die Sonne und den Mond sowie die vier navigationstauglichen Planeten angegeben. Für die Navigation mit Fixsternen wird der ♈︎Grt benötigt, das ist der Grt des Frühlingspunktes. Wird dieser zum mit β angegebenen Sternwinkel eines Fixsterns addiert, dann erhält man den Grt des Fixsterns.
Allerdings sind die Positionen eines Fixsterns gar nicht so fix, wie man früher einmal dachte. So muss auch der Sternwinkel einiger Fixsterne von Jahr zu Jahr neu angegeben werden.
Ein Nautisches Jahrbuch enthält aber noch mehr. Weil die Stundenwinkel nur im Stundenraster angegeben sind, muss auf die Minuten und Sekunden einer Beobachtungszeit interpoliert werden. Dafür stehen am Ende des Buches sogenannte Schalttafeln zur Verfügung, damit auch hier nicht gerechnet werden muss. Wichtig sind auch die Tabellen für eine Sextantenbeschickung. Darüber hinaus wird immer noch die Zeitgleichungstabelle des Jahres angegeben, weiterhin die Fehlerkorrekturen für die Nordsternbreite und vieles andere mehr.
Dieser Aufwand mit den Schalttafeln ist nötig, damit Fehler möglichst vermieden werden. Man musste zwar nicht so viel rechnen, dafür aber umso mehr blättern. Das hatte seine Vorteile besonders für den Fall, dass ein Skipper von Seekrankheit geplagt selbst zu einfachsten Kopfrechenaufgaben nicht mehr in der Lage war.
Die erste deutsche Ausgabe eines Nautischen Jahrbuchs gab es für das Jahr 1852 vom Deutschen Hydrographischen Institut in Hamburg. Die Bezeichnung dieses Amtes wechselte später in Bundesamt für Seeschifffahrt und Hydrographie (BSH). Die letzte Ausgabe erschien im Jahr 2020, womit eine alte Tradition endete.
Die Großschifffahrt benutzt heute nur noch die vollelektronische Satellitennavigation. Unterlagen für eine astronomische Navigation und auch ein Sextant sind in der Großschifffahrt nicht mehr ausrüstungspflichtig, sofern zwei völlig unabhängige vollelektronische Satellitennavigationssysteme an Bord betrieben werden.
Die App Sun Navigation benutzt in der Basic-Version eine Berechnungsroutine, mit der die Sonnenephemeriden aus den Bahnelementen in der Tafel 7.1 und der eingegebenen Beobachtungszeit, bestehend aus Datum und Tageszeit, innerhalb von Millisekunden berechnet werden. Die Pro-Version besitzt eine Datenbank, in der die Sonnenephemeriden bis einschließlich 31. Dezember 2040 gehalten werden. Hier muss weder gerechnet noch geblättert werden.

7.4.4 Ephemeriden der Sonne mit Excel berechnet

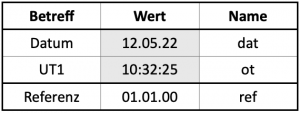
Das MS Office Programm Excel hat wohl jeder auf seinem heimischen PC und damit sollte es möglich sein, Grt und δ für eine beliebige Zeit in diesem Jahrhundert zu berechnen. Das heißt: Wir wollen jetzt die Position berechnen, auf der die Sonne in einer angegebenen Zeit und einem angegebenen Datum im Zenit steht. Wir nehmen auch gleich ein Beispiel, den 12. Mai 2022 um 10:32:25 UT1 (ähnlich UTC).
Wir brauchen dazu lediglich drei kleine Tabellen. Die erste Tabelle, die Tafel 7.4, besitzt drei Zeilen. Die ersten beiden Zeilen dienen zur Eingabe von Datum und Uhrzeit, für die wir die Ephemeriden berechnen wollen. In die dritte Zeile schreiben wir das, Referenzdatum, den 1. Januar 2000. Die Werte der Datenzellen bekommen die Namen dat, ot und ref zugewiesen, die wir dann auch gleich in der dritten Spalte dahinter schreiben.

In der zweiten Tabelle, der Tafel 7.5, legen wir die Bahnelemente der Erde aus der Tafel 7.1 ab.
Das sind die am Referenzdatum herrschenden Werte A und die Koeffizienten B einer darauf folgenden Zeit T. Am praktischsten ist es auch hier, zunächst in der dritten Spalte die Namen zu vergeben. Wir wählen die Namen _A₁ bis _A₄ und _B₁ bis _B4. Der Unterstrich vor den Buchstaben A und B verhindert eine Verwechselung mit den Arbeitsblattzellen A1 bis B4. Die Werte für _A₁ bis _A4 können direkt abgeschrieben werden.

Die Koeffizienten _B₁ bis _B4 müssen dagegen erst noch in Dezimalbrüche umgerechnet werden. Für alle, die mit Excel nur wenig Erfahrung haben, sei das für den Koeffizienten B3 gezeigt, der den Namen _B3 erhalten hat. Man klickt dazu die Zelle links neben dem Namen _B3 an und gibt den in der Tafel 7.1 vor der Zeit T stehenden Bruch ein: =4,2E-7/365,25.

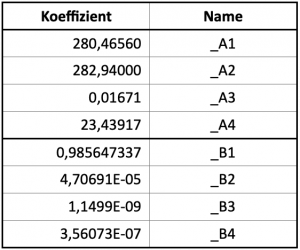
Excel berechnet daraus 1,1499E-09, also eine Dezimalzahl mit der Zehnerpotenz 10^-9. Das wird jetzt auch für alle anderen B-Werte gemacht.
Jetzt müssen wir die von uns vergebenen Namen nur noch Excel mitteilen. Dazu klicken wir auf die Zelle mit der Zahl, für die der Name gelten soll. Beispielsweise klicken wir in der Tafel 7.4 auf die Datumsangabe 12.05.22, denn diesem Datum soll Excel der Name dat mitgeteilt werden. Dann wird in der oberen grünen Funktionszeile die Funktion Formeln angeklickt und darin das Dropdown-Menü Namen definieren. Darin wird dann ebenfalls wieder Namen definieren gewählt. Es öffnet sich ein Fenster, in dem in der Zeile „Geben Sie einen Namen für den Datenbereich ein:“ der Name dat eingetragen und mit OK bestätigt wird.
Dasselbe wird anschließend für alle anderen Zellen wiederholt. Zum Schluss sollten alle Zellen mit den Werten bzw. Koeffizienten nacheinander angewählt werden. Wenn alles richtig gemacht wurde, erscheint für die angewählte Zahl in der Eingabeleiste links oben immer der vergebene Name. Wählt man also die Zelle mit der Zahl 0,0167 an, dann steht ganz oben links in der Ecke der Name _A3.
Als nächstes wird die Rechentabelle eingerichtet, die hier als Tafel 7.6 zu sehen ist. Die Tabelle besitzt 17 Zeilen und drei Spalten. Genau wie bei den vorherigen Tafeln müssen Excel die in der Namensspalte definierten Namen mitgeteilt werden, damit die Formeln in den Werte-Spalte darauf zugreifen können. Sämtliche in der Werte-Spalte von Tafel 7.6 einzutragenden Formeln sind in der für Excel erforderlichen Schreibweise in der Tafel 7.7 angegeben.

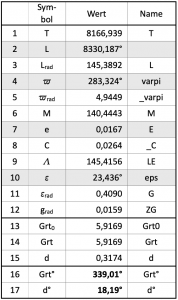
In Zeile 1 wird zunächst erst einmal die Zeit T ausgerechnet. Excel hat dafür eine spezielle Formel, die viel einfacher ist als die in den Gleichungen 7.1 und 7.2 angegebenen allgemeinen Gleichungen. Sie lautet in der Anwendung
=TAGE(dat;ref)+ot-0,5.
Daraus kann Excel nun alle vier Bahnelemente für das Datum und die Tageszeit, wie in Tafel 7.4 angegeben, ausrechnen. Die allgemeine Formel Y = A + B ⋅ T der Bahnelemente in Tafel 7.1 wird in der Werte-Spalte in den Zeilen 2, 4, 7 und 10 (grau hinterlegt) auf die jeweils speziellen Parameter und die Zeit T angewendet. Bis auf den Wert der numerischen Exzentrizität e in Zeile 7 werden die übrigen, jeweils in Grad ausgerechneten Winkel, in der darunter befindlichen Zelle ins Bogenmaß umgerechnet. Zur Umrechnung müssen die Gradmaße aus den darüber liegenden Zellen einfach mit $\pi$ /180 multipliziert werden.  In Excel gibt es dafür auch die Formel W_rad = Bogenmaß(W°). Zu beachten ist, dass die Konstante $\pi$ in Excel immer als PI() angegeben wird. Die Klammern dahinter haben keine weitere Bedeutung.
Die Differenz von mittlerer Länge αm und Länge des Perihels $\varpi$ liefert mit der in Zeile 6 stehenden Gleichung 7.8 die mittlere Anomalie M. Mit ihrem Wert und der numerischen Exzentrizität e aus Zeile 7 rechnet Excel nun mit der in Zeile 8 stehenden Gleichung 7.9 die Mittelpunktsgleichung C aus. In Zeile 14 wird damit die Ekliptiklänge Λ als Summe von C und α_m bzw. L berechnet.
Endlich ist dann alles zusammen, um mit der in Zeile 12 stehenden Gleichung 7.13 die Zeitgleichung g auszurechnen. Daraus folgt dann mit der in Zeile 13 eingetragenen Gleichung 7.14 die Berechnung und Anzeige eines Grt0. Hierbei handelt es sich um einen Wert, der in einem ersten Rechenschritt entstanden ist und einen negativen Überlauf haben könnte. Sollte Grt0 also kleiner als null sein, dann müssen 2 $\pi$ addiert werden. In Zeile 14, die in diesem Fall zur Korrektur dient, steht daraufhin der korrekte Grt im Bogenmaß. Durch Multiplikation mit 180/ $\pi$ , oder in Excel auch mit der Formel Grad von Grt_rad, wird der Greenwichwinkel außerdem in Zeile 16 im Gradmaß angegeben.

Tafel 7.7: in Excel verwendete Formel-Schreibweise

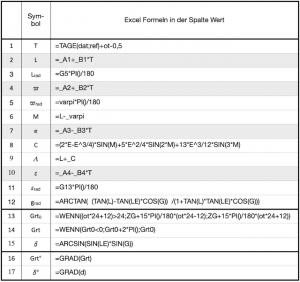
Die Deklinationδ, hier mit dem Namen d bezeichnet, wird mit der Gleichung 7.15 berechnet, die in Excel Schreibweise in Zeile 15 steht. Das Gradmaß der Deklination ergibt sich in derselben Weise nach Multiplikation mit 180/ $\pi$ oder als Grad von Grtrad in Zeile 17.
In Excel gibt es noch eine Besonderheit bei Zeitberechnungen. So wird in der Formel für Grt0 die Tageszeit ot mit 24 multipliziert, was zunächst verwundern mag. Der Grund dafür ist der, dass Excel mit 24 h = 1 rechnet und damit ist 1 Stunde = 1/24 und 12:00 = 0,5. Der außerdem dort verwendete Faktor 15*PI()/180 entspricht (15°/h ⋅ $\pi$ /180) und ist die Winkelgeschwindigkeit der Sonne. Dadurch sieht die Formel in Zeile 13 etwas unübersichtlich aus.

Bild 7.9: Excel Datei zur Berechnung der Sonnenephemeriden.

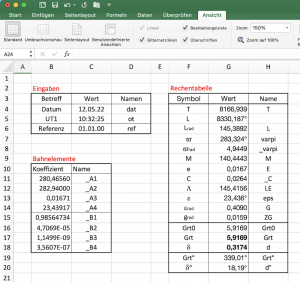
Bild 7.9 zeigt, wie die drei Tabellen in einem Excel-Arbeitsblatt angeordnet sein können. Sie nehmen dort erstaunlich wenig Platz ein.
In der Rechentabelle sind alle Ergebnisse zu sehen, die das in Tafel 7.4 eingetragene Zahlenbeispiel ergibt. Gesucht werden die Ephemeriden Grt und δ für den

12. Mai 2022 um 10:32:25 UT1.

Das Ergebnis steht in den letzten beiden Zeilen der Rechentabelle. Es lautet Grt = 339,01° und δ = 18,19°. eine Umrechnung von Dezimalgrad in Grad und Minuten geschieht dadurch, dass nach Abzug der Gradzahl vor dem Komma die danach erhaltene Differenz mit 60 multipliziert wird, was die Minuten liefert. Allerdings sind dazu mehr als nur zwei Stellen nach dem Komma zu berücksichtigen. Danach erhalten wir

Grt = 339° 0,77’; δ = 018° 11,24’ N.

Diese einfache Berechnungsmethode nach Kepler berücksichtigt nur die Massen von Sonne und Erde. Keine Beachtung finden die Einflüsse des Mondes und der großen Planeten. Deshalb weichen damit berechnete Ephemeriden von der tatsächlichen Position etwas ab. Dadurch entstehende Standortfehler sind jedoch nicht erheblich. Fehler durch nicht sorgfältige Höhen- und Zeitangaben haben meist größere Auswirkungen.