5 & 6 Dead Reckoning und Großkreisrechnung

Links → Kapitel 1, Kapitel 2, Kapitel 3, Kapitel 4, Kapitel 7, Kapitel 8

5 Koppelnavigation

Darunter wird eine einfache und seit Jahrhunderten benutzte Navigationsmethode verstanden. Im Englischen wird sie Dead Reckoning genannt, was totale Berechnung bedeutet. Zur Durchführung verwendet der Navigator einfache, aber zuverlässige Werkzeuge, um drei Dinge zu verfolgen:

  • Kompassrichtung des Bootes,
  • Geschwindigkeit durchs Wasser,
  • Zeit, die auf jede Kursrichtung und jede Fahrtgeschwindigkeit aufgewendet wurde.

Mit diesen Informationen konnte der Navigator Route und Entfernung berechnen, die das Schiff zurücklegt, und in einer Seekarte markieren. Mit einer sorgfältig durchgeführten Koppelnavigation sind Fehlerraten bis herunter zu 5% erreichbar. Das Koppeln wurde früher angewendet, wenn sich das Schiff nachts in komplizierten Gewässern bewegen musste. Das betraf jedoch meist nur Kriegsschiffe. Handelsschiffe gingen in so einem Fall meist vor Anker. Doch wozu brauchen wir heute noch eine Koppelnavigation?

Die astronomische Navigation erfordert zu einer Standortbestimmung mindestens zwei Gestirnshöhen, entweder von zwei verschiedenen Gestirnen oder von einem Gestirn wie der Sonne zu unterschiedlichen Zeiten. Dabei sollten sich die Höhengleichen der beobachteten Gestirne in einem nicht zu spitzen Winkel schneiden. Bei Anwendung des Höhenverfahrens nach Hilaire sollte der Schnittwinkel nicht kleiner als 30° sein, damit der Schnittpunkt der Standlinien noch genau genug herausgelesen werden kann. Schließlich handelt es sich bei Hilaire um ein grafisches Verfahren und früher waren es Bleistiftstriche, die auch mal dicker ausfallen konnten.
Arbeitet man mit Computerunterstützung, dann werden die Schnittpunkte berechnet und eine Strichdicke hätte keine Auswirkung mehr. Trotzdem dürfen auch dort die Kreuzungswinkel nicht zu spitz werden, weil dann schon geringe Abweichungen in der Beobachtung des Kimmabstandes zu größeren Standortabweichungen führen würden. Um einen akzeptablen Schnittwinkel von größer als 25° zu gewährleisten, muss zwischen den Beobachtungen eine ausreichend lange Zeit vergehen.
Wenn nicht gerade Totenflaute herrscht, wird man sich vom Ort der ersten Beobachtung entfernen. Doch mit jeder Entfernungsänderung vom Bildpunkt ändert sich auch die Höhe, in der ein Gestirn beobachtet wird, und das auch dann, wenn es gedanklich geostationär in seiner Position am Himmel eingefroren bleibt. Es geht jetzt also darum, aus den unterschiedlichen Kursen und Strecken zwischen den Beobachtungen einen resultierenden Kurs CMG, eine resultierende Gesamtstrecke über Grund DMG und eine resultierende Geschwindigkeit VMG zu finden. Dabei muss zusätzlich eine eventuell vorhandene Strömung, aber auch ein Versatz durch Wind berücksichtigt werden.

Man wird immer Kurse segeln wollen, in denen der Wind optimal ausgenutzt wird. Beim Segeln mit halbem Wind fällt der scheinbare Wind von der Seite ein. Dieser Zustand ermöglicht die höchste Geschwindigkeit. Das Boot fährt dabei aber nicht in Kielrichtung. Vielmehr ist der Bug etwas in den Wind gedreht, wodurch das anströmende Fahrwasser auf der Leeseite gegen den leicht quer stehenden Kiel und Unterwasserrumpf drückt. Auf diese Weise stellt sich ein Gleichgewicht zwischen Windruck nach Lee und dynamischem Wasserdruck nach Luv her. Der in Kielrichtung weisende Kompass zeigt dann jedoch nicht mehr den Fahrkurs an. Der Wind trifft außerdem die Freibordfläche des Rumpfes und die Aufbauten, die nicht unbedingt zum Kräftegleichgewicht beitragen, und treibt das Boot zusätzlich in Windrichtung ab.
Der Versuch, das alles richtig einschätzen zu können, ist eine Kunst des Skippers. Man kann dies alles nicht wirklich berechnen und die Wirkungen sind bei jedem Bootstyp sowieso unterschiedlich. Werden mehrere Wenden gefahren, dann gleicht sich dieser Effekt sogar aus. Der Skipper oder Navigator wird z. B. bei Nordwind und einer Kompass-Ablesung von 280° einen Fahrkurs von 270° annehmen. Er hat in diesem Fall den Kompasskurs mit -10° beschickt. Letztendlich brauchen wir die Route über Grund und die entsteht nicht allein durch den Bootsantrieb.
Abhängig vom Seegebiet können Meeresströmungen dazu beitragen, dass sich Geschwindigkeit und Kurs von den Anzeigen der Messgeräte an Bord ziemlich unterscheiden. Für eine möglichst genaue Koppelnavigation ist deshalb auch die Berücksichtigung einer Meeresströmung wichtig. Diese entnimmt man speziellen Strömungskarten. Besser ist jedoch die Benutzung eines Meeresströmungs-Radars, das Livedaten liefert. Dazu ist ein Internetzugang erforderlich. Fehlt dieser, dann könnte man jemanden via Satellitentelefon anrufen, der einem die Daten mitteilt. Bei Benutzung analytischer Navigationsmethoden kann die Zeitspanne zwischen zwei Beobachtungen etwas kürzer gehalten werden, weil diese genauer rechnen. In strömungsarmen Gebieten entsteht dadurch kaum ein nennenswerter Fehler. Trotzdem soll nachfolgend gezeigt werden, wie eine gekoppelten Strecke unter Berücksichtigung von Meeresströmungen berechnet wird.

5.1 Zwei Geschwindigkeiten

Ein Schlag ist im Weiteren definiert als eine gleichmäßig gefahrene Strecke in einem bestimmten Kurs. Das bedeutet, dass ein neuer Schlag immer nach einer Wende, einer Halse, einer nachhaltigen Geschwindigkeitsänderung oder einer nachhaltigen Kursänderung beginnt. Auf die Länge bzw. Distanz eines Schlages und auf den gefahrenen Kurs dieser Strecke nehmen der Bootsantrieb, aber auch die Stärke einer Meeresströmung Einfluss.

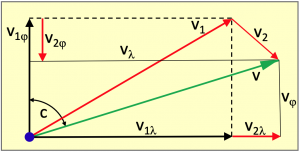
Bild 5.1: vektorielle Addition der Geschwindigkeiten von Bootsantrieb und Strömung.

Bild 5.1 zeigt den Zusammenhang. So findet die vom Bootsantrieb erzeugte Geschwindigkeit v1 durch das Wasser in einem Strömungsfeld statt, das mit der Geschwindigkeit v2 in eine andere Richtung driftet. Die daraus resultierende Geschwindigkeit v wird dadurch erhalten, dass die beiden Vektoren v1 und v2 aneinandergesetzt werden.
Der resultierende Kurs c, auf dem sich das Boot dann bewegt, ist der Winkel zwischen der Nordrichtung v1φ und dem Geschwindigkeitsvektor v. Im Bild wird die vom Bootsantrieb generierte Geschwindigkeit nach Osten durch die Strömung um v2λ vergrößert und die nördlich gerichtete Geschwindigkeit um v2φ vermindert.

 

5.2 Addition der Schläge

Die jeweiligen Distanzen sind die Produkte von Geschwindigkeit v und Zeitdauer t. Da für eine Gesamtbewertung nur die Summe aller Nord-Süd-Abschnitte und die Summe aller Ost-West-Abschnitte gebraucht werden, egal wie viele Wenden oder Halsen gefahren wurden, müssen diese zunächst definiert werden. Mit dem Zählindex i für jeden Schlag, also i = 1 bis n, wenn n Schläge gefahren wurden, gelten zunächst:

(5.1)   \[\Delta\varphi_i=t_i\,(\text{v}_{Ai}\cos c_{Ai}+\text{v}_{ci}\cos c_{ci}),\]

(5.2)   \[\Delta\lambda_i=t_i\,(\text{v}_{Ai}\sin c_{Ai}+\text{v}_{ci}\sin c_{ci})\cdot\]

Hierin gelten für jeden einzelnen Schlag:

            i         Nr. des gefahrenen Schlages
          
 Δφi      Nord-Süd Komponente

          Δλi       Ost-West Komponente

           ti         Zeitdauer in Stunden

          vAi       Kurs durchs Wasser in Grad 

          cAi       Antriebsgeschwindigkeit

          vCi      Strömungsgeschwindigkeit

          cCi      Strömungsrichtung

Die Abschnitte gemäß den Gleichungen 5.1 und 5.2 werden jetzt für jeden Schlag getrennt addiert und man erhält die gesamt zurückgelegten Distanzen jeweils in Nord-Süd und in Ost-West Richtung.
Für den total zurückgelegten Nord-Süd Abschnitt schreibt sich dann:

    \[\Delta\varphi_T=\Delta\varphi_1+\Delta\varphi_2+\Delta\varphi_3+ ...\Delta\varphi_n =\]

    \[=\sum_{i=1}^n \varphi_i\cdot\]

Für den totalen Ost-West Abschnitt gilt in der gleichen Weise:

    \[\Delta\lambda_T=\Delta\lambda_1+\Delta\lambda_2+\Delta\lambda_3+ ...\Delta\lambda_n =\]

    \[=\sum_{i=1}^n \lambda_i\cdot\]

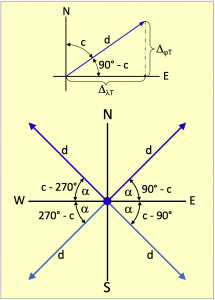
Geometrisch gesehen bilden diese Strecken ein rechtwinkliges Dreieck, wie es in der oberen Hälfte von Bild 5.2 für den ersten Quadranten dargestellt ist. Die Katheten sind darin jeweils die Summen aller gefahrenen Nord-Süd- bzw. Ost-West-Komponenten. Die dabei total zurückgelegte Distanz über Grund d (DMG) wird daraus einfach nach dem Satz des Pythagoras berechnet:

Bild 5.2: Ableitung der Kurswinkel in den vier möglichen Quadranten.

(5.3)   \[\text{d}^\circ=\sqrt{(\Delta \varphi_T )^2+(\Delta \lambda_T )^2}\cdot\]

Im Bild ist aber auch der dabei gefahrene Kurs c (CMG) eingetragen. In einem rechtwinkligen Dreieck berechnet sich der Tangens eines Winkels bekanntlich als Quotient von Gegenkathete und Ankathete. Wir erhalten also:

    \[\tan(90^\circ-c)=\frac{\Delta\varphi_T}{\Delta\lambda_T}\]

Die Arkustangensfunktion liefert direkt den Winkel, also 90° – c, und wir erhalten

    \[90^\circ-c=\arctan\frac{\Delta\varphi_T}{\Delta\lambda_T}\]

sowie endlich

    \[c=90^\circ-\arctan\frac{\Delta\varphi_T}{\Delta\lambda_T}\]

Im zweiten Quadranten berechnet sich der Winkel zwischen einem Breitenkreis und dem Versegelungsvektor, wir nennen ihn zunächst α, mit

    \[\alpha=\arctan\frac{\Delta\varphi_T}{\Delta\lambda_T}\]

Ein Kurs im zweiten Quadranten muss deshalb mit c = 90° + α angegeben werden. Dafür wird geschrieben:

    \[c=90^\circ+\alpha=90^\circ+ \arctan\frac{\Delta\varphi_T}{\Delta\lambda_T}\]

Im zweiten Quadranten ist die Summe aller Breitenänderungen negativ und der Kurs ist südöstlich. Damit ist auch der Arkustangens negativ und die Addition in der vorstehenden Gleichung wird zu einer Subtraktion. Aus diesem Grund gilt für die Quadranten 1 und 2 dieselbe Berechnungsformel und das ist die obere in der Gleichung 5.4. Sie gilt für Kurse mit einer östlichen Komponente. Da α der Winkel zwischen Breitenkreis und Versegelungsvektor ist, wird dieser Winkel α im unteren Teil von Bild 5.2 mit c – 90° eingetragen.

(5.4) 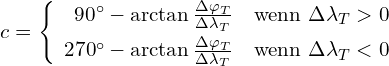  \begin{equation*}c=\left\lbrace\;\;\; 90^\circ-\arctan\frac{\Delta\varphi_T}{\Delta\lambda_T}\phantom{11}\text{wenn }\Delta\lambda_T>0\atop\ 270^\circ-\arctan\frac{\Delta\varphi_T}{\Delta\lambda_T}\phantom{11}\text{wenn }\Delta\lambda_T<0\end{equation*}

Dieselben Betrachtungen können nun auch für Kurse mit westlichen Komponenten angestellt werden. Dabei wird sich dann zeigen, dass der Arkustangens nun von 270° abgezogen werden muss, wie es die untere Formel in Gleichung 5.4 angibt. Die Hilfswinkel im Bild betragen dann 270° – c und c – 270°.

5.3 Das Koppelboard

Hierbei handelt es sich um ein Hilfsmittel, auf dem der Rudergänger für jeden gefahrenen Schlag Kurs, und Geschwindigkeit mit der zugehörigen Zeit einträgt. Nach jeder signifikanten Änderung von Kurs oder Geschwindigkeit entsteht so eine neue Zeile. Aus diesen Einträgen lässt sich dann auf einer Karte ein Track konstruieren, wodurch der aktuelle Standort auch zwischen den Beobachtungen immer bekannt ist. Ein von der Navigations-App in Kapitel 2 angelegtes Koppelboard ist im Bild 2.16 zu sehen.

Tafel 5.1: Koppelboard

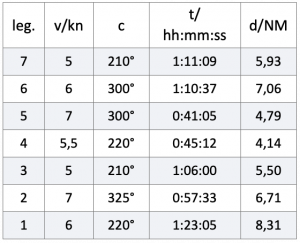
Wie die vorhandenen Zahlen verarbeitet werden, soll abschließend noch an einem Beispiel aufgezeigt werden. Die folgende Tabelle enthält dazu sieben Zeilen mit jeweils einem zu behandelnden Schlag. Der Unterschied zwischen Schlag 3 und 4 besteht in einer Kurskorrektur, um beispielsweise den Wind optimaler nutzen zu können. Die Eintragung eines Schlages 6 auf gleichbleibendem Kurs war nötig, weil die Geschwindigkeit dauerhaft um 1 kn gefallen war. Die nachfolgende Tafel enthält alle eingetragenen Werte eines mehr als sieben Stunden dauernden Törns.
Man kann sehen, dass insgesamt vier Wenden gefahren wurden. In den dabei absolvierten Schlägen wurde eine Strecke durch das Wasser von 42,45 NM zurückgelegt, was die Summe der in der letzten Spalte angegebenen Einzeldistanzen aussagt.
Zu bestimmen sind jetzt die dabei gutgemachte Distanz über Grund DMG, der dabei gefahrene mittlere Kurs CMG und die daraus resultierende Geschwindigkeit VMG. Die Tafel 5.2 listet für jeden Schlag die gefahrene Breitenänderung und Längenänderung gemäß den Gleichungen 5.1 und 5.2. auf.
Eventuell vorhandene Strömungen werden in diesem Beispiel nicht berücksichtigt. Daraus kann jetzt mit der Gleichung 5.3 die DMG berechnet werden und wir schreiben

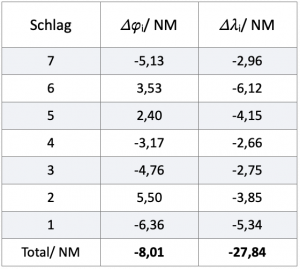
Tafel 5.2: Breitenkomponenten und Längenkomponenten des gefahrenen Törns

    \[d=\sqrt{8,01^2+27,84^2}=\underline{\underline{28,97 NM}}\cdot\]

Die λ-Spalte besitzt in der Summe ein negatives Ergebnis, also muss der mittlere Kurs CMG mit der unteren Formel in der Gleichung 5.4 ausgerechnet werden. Es ergibt sich demnach:

    \[c=270^\circ-\arctan\frac{-8,01}{-24,84}= \underline{\underline{254^\circ}}""\cdot\]

Die mittlere Geschwindigkeit VMG ist der Quotient aus der gutgemachten Distanz d und der Gesamtzeit des Törns von 7:14:41 h und wir erhalten:

    \[\overline{\text{v}} =\frac{28,97\; NM}{7,245\;h}=\underline{\underline{4\;kn }}\cdot\]

Das Ergebnis des Törns ist folgendermaßen zusammengefasst:

    1. Dauer des Törns 7:14:41 h
    2. Fahrt durchs Wasser 42,45 NM
    3. DMG = 28,97 NM
    4. CMG = 254°
    5. VMG = 4 kn

Im Bild 5.3 sind die einzelnen Schläge in einer Grafik dargestellt.

Von der App werden die in 3. bis 5. aufgeführten Ergebnisse im Minutentakt neu berechnet, zur Anzeige gebracht und abgespeichert. Die aktuellen Versegelungsdaten stehen deshalb nach jeder zweiten Beobachtung sofort, das heißt minutengenau zur Verfügung. Eventuell vorhanden Strömungsdaten werden von den Gleichungen 5.1 und 5.2 nur solange erfasst, wie sie in den Eingabefeldern sichtbar eingetragen sind.

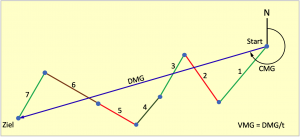
Bild 5.3: Grafik eines gekoppelten Törns über mehr als 7 Stunden

Koppelnavigationen wurden in der Praxis bisher immer nur grafisch ausgeführt. Es wäre auch ziemlich aufwendig, eine Versegelung mit den Gleichungen 5.1 bis 5.4 immer berechnen zu wollen. Oft wurden die Versegelungen auch nur geschätzt. Soll jedoch ein sauber arbeitendes Navigationsprogramm erstellt werden, dann wird man den hier gezeigten analytischen Weg gehen müssen. Aus diesem Grunde sind die Formeln und ihre Herleitung hier beschrieben.

 

 

6 Großkreisrechnung

Bei kleinen Entfernungen wird der Skipper meist einen direkten Kurs wählen. Auf einer 2-D-Karte ist das eine gerade Linie von A nach B. Solch ein Weg folgt einer sogenannten Loxodrome. Dabei werden die Meridiane, auf einer 2-D-Karte sind das die senkrechten Linien, immer im gleichen Winkel geschnitten. Da auf einem Globus der Abstand zwischen den Meridianen zu den Polen hin immer enger wird, besitzt ein solcher Kurs, wenn er nur lange genug verfolgt wird, eine Spiralform bis zum Pol. Grundsätzlich ist ein dabei zurückgelegter Weg von A nach B nicht optimal kurz, denn die kürzeste Verbindung zwischen zwei Punkten auf einer Kugeloberfläche führt entlang eines Großkreises. Es war Pedro Nunes, der im Jahre 1550 als Erster Untersuchungen in dieser Richtung anstellte.

Bild 6.1: Distanz d und Anfangskurs c einer Orthodrome von A nach B.

Als es vor langer Zeit noch nicht möglich war, den Längengrad zu bestimmen, segelte man zunächst an einer bekannten Küste entlang nach Norden oder Süden, bis zum gewünschten Breitengrad, und begann dann erst die Überfahrt nach Westen oder Osten. Dabei verließ man den Breitengrad nicht, was regelmäßig durch die Bestimmung der Mittags- oder Nordsternbreite gesichert wurde.
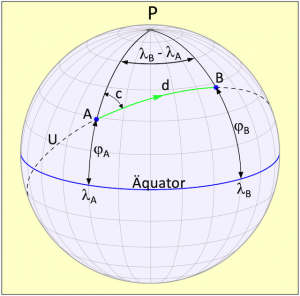
Auch ein solcher Kurs ist nicht optimal kurz, denn er erfolgt längs eines Breitenkreises und ein Breitenkreis kann auf einer Kugeloberfläche nicht die kürzeste Verbindung zwischen zwei Punkten sein. Die kürzeste Verbindung zwischen zwei Punkten auf der Erdkugel geht immer längs einer Großkreislinie, denn diese hat ihren Mittelpunkt im Mittelpunkt der Kugel. Eine auf einem Großkreis abgefahrene Strecke wird als Orthodrome bezeichnet. Eine Orthodrome ist im Bild 6.1 die grün dargestellte Verbindung von A nach B.
Es ist eine Sache der Wirtschaftlichkeit, dass möglichst immer der schnellste und direkteste Kurs gefahren wird. Dies dauert weniger lang und mit zunehmender Anzahl an Dampfschiffen wurde auch jede Menge Brennstoff eingespart. Manch einer mag sich schon einmal gewundert haben, warum Flugzeuge bei Langstreckenflügen einen derart großen Bogen machen und nicht direkt zum Ziel fliegen. Sie folgen einer Orthodrome und das ist auf einer Kugel immer der kürzeste und direkte Weg.
Als Segler möchte man auf langen Strecken sein Ziel ebenfalls auf dem kürzesten Weg erreichen und deshalb wollen wir hier kurz darauf eingehen. Man kann diesbezüglich zwar sehr viel rechnen, aber ich meine, dass es genügen dürfte, seinen Anfangskurs festlegen zu können, und dass man weiß, wie lang ein kürzester Weg von A nach B ist. Ein End-Kurs kann mathematisch zwar auch bestimmt werden. Doch wo läge hier der Sinn? Lieber sollte man unterwegs von Zeit zu Zeit die Anfangskursbestimmung wiederholen. Mit der in Kapitel 2 vorgestellten App funktioniert das mühelos.
Die Berechnungen erfolgen mithilfe des Kosinus Seitensatzes. Die im Bild 6.1 gezeigten Meridianabschnitte PA und PB sind bekannt und ebenso der davon eingeschlossene Polwinkel λB – λA, denn man kennt schließlich die Positionen von Standort und Zielort. Daraus lässt sich dann die Distanz d einfach berechnen. Durch die Verwendung der Komplemente φA für PA und φB für PB drehen sich Sinus in Kosinus und umgekehrt. Danach gilt für die Distanz:

(6.1)   \[\text{d}^\circ=\arccos\big[\sin\varphi_A\sin\varphi_B+\cos\varphi_A\cos\varphi_B\cos(\lambda_B-\lambda_A)\big]\cdot\]

Jetzt sind alle Seiten des Dreiecks bekannt und damit kann jeder Winkel im Dreieck berechnet werden. Der Anfangskurs c errechnet sich wie folgt:

(6.2)   \[c^\ast=\arccos\frac{\sin\varphi_B-\sin\varphi_A\cos d}{\cos\varphi_A\sin d},\]

(6.3)   \begin{equation*}c_A=\left\lbrace \;\;\;\phantom{40}c^\ast\phantom{40}\;\;\text{ wenn }\lambda_A<\lambda_B\atop\ 360^\circ-c^\ast\;\;\text{wenn }\lambda_A>\lambda_B\cdot\end{equation*}

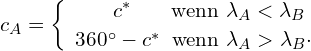
Die Zusatzformel 6.3 regelt einen Unterschied zwischen Ost- und Westkurs. Bei einem Ostkurs ist der Anfangskurs gleich c*. Bei einem Westkurs muss c* von 360° subtrahiert werden, um den Anfangskurs zu erhalten.
Zum Abschluss folgt noch ein Beispiel. Ein Boot beabsichtigt, die kürzeste Strecke von Charleston (NC) 32,73° N / 79,83° W und Lissabon 38,64° N / 9,31° W zurückzulegen.

Tafel 6.1: Berechnungsbeispiel

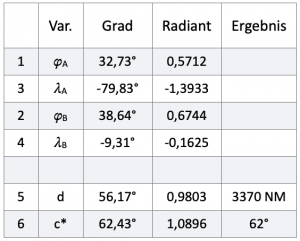
Tafel 6.1 enthält dazu alle Zahlenwerte. In den Zeilen 1 bis 4 stehen die Koordinaten von Start- und Zielort. Die Rechenergebnisse finden sich in den Zeilen 5 und 6. Die Werte sind in Grad und Radiant angegeben. Programme auf Computern und auch Tabellenkalkulationen rechnen mit Winkeln im Bogenmaß, die hier in der Spalte Radiant angegeben sind. Zur Erinnerung: 360° = 2\pi
Der Bogen d ist ein Winkel im Erdinnern mit einer Größe von 56,17° wie das im Bild 4.1 auf der rechten Seite gezeigt wurde. Da ein Grad auf der Erdoberfläche eine Bogenlänge von 60 nautischen Meilen aufspannt, ergibt sich die Bogenlänge von d als Produkt von 56,17° ⋅ 60 NM/Grad und damit zu 3370 NM.

Schreibe einen Kommentar

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert