3 Kleine Sextantenkunde

Links → Kapitel 1, Kapitel 2, Kapitel 4, Kapitel 5 und 6, Kapitel 7, Kapitel 8

Ein Sextant ist nichts weiter als ein präzises optisches Winkelmessgerät. Der Navigator braucht es, damit er den Höhenwinkel zwischen der Kimm und dem Mittelpunkt eines Himmelskörpers auf Bruchteile einer Bogenminute genau messen kann. Ziel dieser Messung ist die Feststellung der Entfernung zwischen dem Standort eines Beobachters und dem Ort auf der Erde, an dem der beobachtete Himmelskörper gerade im Zenit steht. Abhängig vom Können des Navigators und der Präzision des Instrumentes kann diese Distanz mit einer Genauigkeit von bis zu +500 m bestimmt werden. Doch schon bei geringstem Seegang ist diese Genauigkeit nicht mehr erreichbar.

3.1 Aufbau eines Sextanten

Den grundsätzlichen Aufbau eines Sextanten zeigt Bild 3.1. Seine Hauptbestandteile sind der Rahmen mit Gradbogen und Griff, die schwenkbare Alhidade und das Teleskop. Auffallend sind dann noch die Spiegel und zahlreiche Schattengläser. Es ist also ein sehr beeindruckendes Instrument. An Bord wird der Sextant in einer stabilen Holzkiste – meist aus Mahagoni – aufbewahrt, in die er nach jeder Messung wieder gebracht werden sollte. Diese Kiste ist möglichst fest an einem gut erreichbaren Platz an einer Wand anzubringen. In der Kiste befindet sich weiteres Zubehör zur Pflege des Instruments. Die Kiste sollte so beschaffen sein, dass der Sextant im Gebrauchszustand darin verwahrt werden kann, also ohne vorher alle Schattengläser zurückklappen zu müssen.

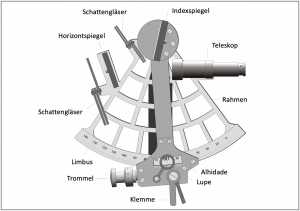
Der Griff besteht meistens aus Holz und ist fest mit dem Rahmen verbunden. Im Griff befindet sich meist auch der Platz für eine Batterie zur Beleuchtung, damit der Winkel auch in der Dämmerung abgelesen werden kann.

Der Rahmen oder Körper eines Sextanten wird klassischerweise aus Bronze oder Messing angefertigt. Ein heute weit verbreitetes Material ist Aluminium, weil es leicht ist. Bei sehr hochwertigen Instrumenten kommt aber immer noch Bronze zur Anwendung. Die Farbe des Rahmens ist meist schwarz. Weiß lackierte Sextanten haben den Vorteil, dass sie sich bei längerer Sonneneinstrahlung nicht zu sehr aufheizen können. Dadurch kann sich der Rahmen auch nicht verziehen, was der Messgenauigkeit zugutekommt. Sextanten werden mit Toleranzen von 1/1000 mm gebaut. 
Jede unnötige Aufheizung in der prallen Sonne und jeder Stoß kann die Messgenauigkeit beeinträchtigen. Seit einiger Zeit werden Sextanten auch aus Plastik hergestellt. Zur Anwendung kommen dabei glasfaserverstärkte Kunststoffe. Sie sind sehr leicht und können damit sogar windempfindlich sein.

Als Limbus bezeichnet man den Gradbogen mit der Winkelskala. Dieser ist auf dem Rahmen aufgebracht. Die Einteilung überstreicht dabei einen Winkelbereich von mindestens 120 Grad. Auch Winkel unter null Grad müssen messbar sein, um beispielsweise einen negativen Indexfehler erfassen zu können. Die Gleichmäßigkeit der Skala und ihre Klarheit vermitteln einen ersten Eindruck von dem Instrument. Immerhin verkörpert der Abstand zwischen zwei Teilstrichen, der etwas mehr als 1 mm beträgt, eine Entfernung von 60 Seemeilen auf der Erdoberfläche.

Die Alhidade ist der bewegliche Arm des Instruments. Im Drehpunkt der Alhidade befindet sich der Indexspiegel und am unteren Ende die Mikrometertrommel oder ein Nonius. Um die Alhidade bewegen zu können, muss ihre Klemme gelöst werden. Die Alhidade muss sich leicht bewegen lassen und dabei einen ausgesprochen stabilen Eindruck hinterlassen. Bei Plastiksextanten neigt die Alhidade zu Haftreibungen. Sollte dies der Fall sein, dann gleitet sie nicht, sondern springt etappenweise. Etwas Vaseline kann hier Abhilfe schaffen.

Die Trommel ermöglicht eine Feineinstellung und bewegt die Alhidade mit jeder Umdrehung um ein Grad weiter. Die Unterteilung auf der Trommel geht deshalb von 0 bis 60 Bogenminuten. Ein fest angebrachter Nonius ermöglicht das Ablesen von Bruchteilen einer Bogenminute, was auf kleineren Schiffen wohl kaum einen praktischen Nutzen haben dürfte. Wer es hier bei Seegang auf zwei Bogenminuten Genauigkeit schafft, der darf sich als Könner bezeichnen, denn das sind zwei Seemeilen Ungenauigkeit. Bei Präzisionssextanten erreicht die Einstellgenauigkeit sogar zehn Bogensekunden, was dann einige hundert Meter mehr oder weniger in der Entfernung zum Bildpunkt ausmachen.
Sogar Plastiksextanten besitzen eine Einstellgenauigkeit von 20 Bogensekunden, doch Einstellgenauigkeiten sind nicht identisch mit der Messgenauigkeit. Billige Plastiksextanten haben keine Trommel, sondern nur einen Nonius, der eine Einstellgenauigkeit von einer Bogenminute ermöglichen soll. Das wäre dann eine Seemeile. Eine exakte Einstellung eines Höhenwinkels ist mit derartigen Geräten nahezu unmöglich. Plastiksextanten mit einer Noniusskala eignen sich nicht für eine seriöse Navigation. Sie können jedoch in einem Notfall hilfreich sein, dass man überhaupt den Weg in die Heimat zurückfinden kann.

Das Teleskop dient zur gleichzeitigen Betrachtung vom Spiegelbild der Sonne und Horizont. Beides zusammen wird bei richtiger Einstellung der Alhidade auf dem Horizontspiegel sichtbar. Üblich sind hier Teleskope von 4 x 40, also mit vierfacher Vergrößerung. Bei Seegang wünscht man sich allerdings eine kleinere Vergrößerung, damit die Sonne nicht so leicht aus dem Sichtbereich verschwinden kann. Teleskope mit 2,4 x 25 stellen hier die bessere Alternative dar. Teleskope können leicht abgeschraubt werden und sind manchmal auch wechselbar.

Horizontspiegel gibt es als Halbsicht- und Vollsichtspiegel. Bei Halbsichtspiegeln ist nur die rechte Hälfte voll verspiegelt und die linke Hälfte besteht aus durchsichtigem Glas. Traditionell blieb die linke Seite sogar offen, sodass dort der Horizont besonders gut sichtbar war. Vollsichtspiegel sind schwach verspiegelt und gleichzeitig durchsichtig. Bei diesen spiegelt sich die Sonne sehr gut und auch der Horizont scheint noch gut durch. Vollsichtspiegel eignen sich zur Navigation mit der Sonne am besten. Sextanten mit Halbsichtspiegeln sind zur Navigation mit Sternen recht gut geeignet, weil der Horizont etwas klarer gesehen werden kann. Anfänger sollten auf jeden Fall zu Instrumenten mit einem Vollsichtspiegel greifen.

Schattengläser dienen dem Blendschutz und können in den Strahlengang eingeschwenkt werden. Sie sind in der Regel grau und farblich getönt. Üblich sind vier Indexschattenfilter und drei Horizontschattenfilter, die alle unterschiedliche Filterwirkungen aufweisen. Die Gläser sollten auf jeden Fall durchgefärbt und nicht beschichtet sein. Kratzer in den Beschichtungen lassen das Sonnenlicht ungefiltert durch, was zum einen sehr störend sein kann, zum anderen aber nicht gut für die Augen ist. Das Material von Schattengläsern muss optisch hochwertig sein und darf den Strahlengang nicht beeinflussen. Dünne Gläser sind hier zwar von Vorteil, aber auch empfindlicher. Hochwertige Sextanten verwenden polarisierende Schattengläser, um damit Spiegelungen auf der Wasseroberfläche zu reduzieren.

3.2 Funktionsweise

Wie im Bild 3.2 zu erkennen ist, existieren in einem Sextanten zwei Strahlengänge, die sich im Fernrohr vereinen. Ein direkter Strahlengang, der als blaue Linie dargestellt ist, geht vom Horizont geradewegs durch den Horizontspiegel hindurch ins Fernrohr.
Ein umgelenkter Strahlengang, der als rote Linie eingezeichnet ist, geht von dem beobachteten Objekt Sonne aus, wird vom Indexspiegel auf den Horizontspiegel reflektiert und gelangt dann ebenfalls infolge einer weiteren Reflexion ins Fernrohr des Betrachters.

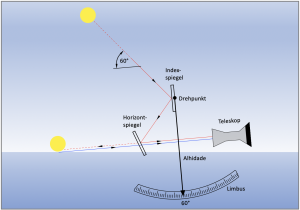
Je nach Stellung der Alhidade können so zwei verschiedene Objekte, die vom Betrachter aus gesehen in einem Winkel zueinanderstehen, in einem Bild direkt neben- oder übereinander dargestellt werden. Die Stellung der Alhidade zeigt diesen Winkel auf dem Gradbogen des Instruments an.
Bei einem Vollsichtsextanten ist der Horizontspiegel halbdurchlässig. Man kann darauf sowohl die Kimm als auch die Scheibe der Sonne sehen, wie es Bild 3.3 zeigt.

 

Bei einem traditionell gebauten Halbsichtsextanten existiert ein Horizontspiegel nur in der rechten Hälfte des Sichtfeldes und ist undurchsichtig. Die andere Hälfte ist dagegen vollkommen frei und man kann direkt auf den Horizont sehen. Es ist üblich, dass die freie Hälfte aus durchsichtigem Glas besteht. Das hat den Vorteil, dass die Kimm besser sichtbar ist, so bei der Beobachtung von Sternen in der Dämmerung. Nachteilig ist, dass eine präzise Berührung des Unterrandes der Sonne mit dem Horizont insbesondere beim Schwenken ein gut schätzendes Auge erfordert. Die Art und Weise, wie Sonne und Kimm in einem Halbspiegelsextant erscheinen, wird im Bild 3.4 gezeigt.

3.3 Messvorgang

Eine präzise Kimmabstandsmessung hängt in erster Linie nicht von der Genauigkeit des Instrumentes, sondern von der Übung des Navigators ab. Messungen bei Seegang sind schon sehr anspruchsvoll und auch der Geübte ist erleichtert, wenn er eine Messung mit gutem Gewissen beenden konnte.
Wir bleiben zunächst bei der Sonne: Der Sextant muss zunächst in ihre Richtung gebracht werden. Das gestaltet sich schon nicht ganz einfach. Man braucht dazu einen festen Stand. Dabei darf man sich auch nicht in Gefahr begeben. Die Sonne sollte ebenfalls gut erkennbar sein. Sie sollte dazu querab oder achteraus hereinschauen. Wenn es notwendig ist, sollte im Sinne einer möglichst genauen Messung der Kurs geändert werden, damit Ruhe ins Schiff kommt oder die Richtung zur Sonne optimal bzw. sogar beides erreicht wird.
Die einzuschwenkenden Schattengläser sollten bekannt sein. Neulinge müssen hier ein wenig experimentieren. Werden am Anfang gleich die dunkelsten Gläser gewählt, dann findet man unter Umständen erstmal gar nichts. Bei Seegang schaukelt das Schiff nicht nur, es dreht sich auch immer ein wenig hin und her. Dann ist es gar nicht so einfach, die mühsam gefundene Sonne im Sichtfeld des Teleskops zu behalten – vor allem wenn das Teleskop eine zu starke Vergrößerung hat. Sobald die Sonne gefunden worden ist, sollten die Schattengläser ausgewählt und das Teleskop scharf gestellt werden. Die Sonne muss als klare Scheibe mit scharfem Rand erscheinen und der Horizont sollte als scharfe Linie erkennbar sein.
Der Kimmabstand ist die senkrechte Verbindungslinie und damit die kürzeste Verbindung zwischen Sonnenmitte und Kimm. Da es aber unmöglich ist, den Sextanten immer genau senkrecht zu halten, muss ein Trick angewendet werden, der darin besteht, ihn leicht um seine Horizontalachse zu schwenken. Dabei pendelt das Bild der Sonne im Teleskop, wie es im Bild 3.5 zu sehen ist. Erst wenn die Sonne in der tiefsten Pendelposition die Kimm gerade noch berührt, stimmt die eingestellte Höhe. Man sagt dazu auch, dass die Sonne die Kimm küsst. Wenn die Sonne am Vormittag noch steigt, kann mit der Trommel eine Höhe eingestellt werden, bei der der Unterrand der Sonnenscheibe noch ein wenig ins Wasser eintaucht. Nun braucht man nur noch zu pendeln. Dabei steigt die Sonne und taucht in Sekundenschnelle aus dem Wasser heraus. Sobald die Sonnenscheibe die Kimm gerade noch schrammt, wird „Stopp“ gerufen, damit ein Helfer eine Stoppuhr anhalten kann, die zu einer vollen Minute einer Uhr mit der Universalzeit UTC gestartet wurde. Die sekundengenaue Messzeit kann daraufhin problemlos bestimmt werden.
Wird die Höhe nachmittags gemessen, dann wird die Trommel so eingestellt, dass die Sonnenscheibe ein wenig über der Kimm zu sehen ist. Anschließend wird nur noch gependelt. Dabei kann sehr gut beobachtet werden, wie die Sonne sinkt. Im entscheidenden Moment wird auch hier „Stopp“ gerufen, damit ein Mitsegler die Stoppuhr anhält.
Es ist wichtig, dass die Kimm auch immer sichtbar ist. Bei sehr hoher Dünung ist die Kimm aus einem Wellental heraus womöglich nicht erkennbar. Grundsätzlich sollte eine Beobachtung stets auf dem Kamm einer Welle beendet werden und nicht im Wellental, denn der Horizont wird aus Wellenkämmen gebildet. Da Wellenhöhen nur sehr schlecht geschätzt werden können, ist eine genaue Abschätzung der momentanen Augeshöhe leider unmöglich.

 

3.4 Wann kann gemessen werden?

Das zu beobachtende Gestirn und die Kimm müssen gleichzeitig sichtbar sein. Das ist am Tag bei der Sonne immer der Fall, sofern sie nicht gerade von Wolken verdeckt oder von einem Dunstschleier umgeben ist. Die Sonnenscheibe sollte immer klar erkennbar sein.
Sterne können nur in der Dämmerung früh am Morgen oder nach Sonnenuntergang am Abend beobachtet werden. In der Dunkelheit steht kein Horizont zur Verfügung. Es sollte sich ebenfalls an die Regel gehalten werden, dass die Sonne nur gemessen wird, wenn sie höher als 15°, besser sogar 25° steht. Bei Anwendung der Hilaire-Methode inklusive der Tafelmethode darf die maximale Höhe 80° – andere sagen 70° – nicht übersteigen. Bei Benutzung der hier beschriebenen analytischen Methoden, mit denen ein Standort direkt aus den Höhenkreisen bestimmt wird, und auch bei der hier im Kapitel 2 präsentierten App besteht keine obere Grenze.
Die Einhaltung einer Untergrenze ist der Wirkung der Refraktion geschuldet. Die Beugung des Lichts (siehe Bild 3.6) durch die Atmosphäre ist bei kleinen Kimmabständen groß, weil das Licht lange Strecken durch die Atmosphäre nehmen muss. Die dadurch entstehenden Fehler können nur durch eine nachträgliche Korrektur des am Sextanten abgelesenen Winkels berichtigt werden.
Die zweite Forderung, dass eine maximale Höhe nicht überschritten werden darf, betrifft nur einen Nachteil in der Hilaire-Methode, bei der ein Standort geschätzt werden muss. Dabei wird das für den Schätzort berechnete Azimut nur angenähert mit dem Azimut des Standortes übereinstimmen. Schätzort, Standort und Bildpunkt der Sonne werden kaum alle drei auf der Linie des berechneten Azimutstrahls liegen. Wenn sich der Standort querab vom Azimutstrahl befindet, wirken sich die Krümmungen der Höhenkreise sehr stark auf das berechnete Standortergebnis aus. Je höher die Sonne beobachtet werden kann, desto kleiner sind die Durchmesser der Höhenkreise und der Einfluss der Krümmungen nimmt zu. 
Bei Beobachtungen der Sonne darf diese nicht von Wolken verhangen sein. Es kann sein, dass nur der Unter- oder der Oberrand von Wolken verdeckt ist. In dem Fall ist in dem Programm, das zur Berechnung des Standortes benutzt wird, die entsprechende Einstellung für „Sun at“ zu wählen. Leichte dunstige Schleierwolken können mitunter zugelassen werden. Das ist davon abhängig, ob es möglich ist, die Sonnenscheibe mithilfe geeigneter Schattengläser und Teleskopeinstellungen klar erkennbar zu machen.
Eine weitere Frage ist, zu welchem Zeitpunkt Höhenmessungen zur Standortbestimmung am zweckmäßigsten erfolgen sollten. Eine alte Regel lautet, dass die Zeitpunkte so weit auseinanderliegen sollten, dass der Schnittwinkel zwischen den Höhenkreisen kein spitzer ist und nicht kleiner als 30° sein darf. In der Literatur findet man auch die Aussage, dass eine Vormittags- und eine Nachmittagsmessung günstig wären.
Dies lässt sich jedoch nicht verallgemeinern. Wenn im 19. und 20. Jahrhundert ein Standort ohne elektronische Rechenhilfe bestimmt werden sollte, dann wurde auf solche Dinge mehr geachtet, denn nach einer Beobachtung musste immer sehr lange gerechnet werden. Die Zahl der Beobachtungen hielt sich deshalb in Grenzen. Die direkten Verfahren berechnen einen Standort innerhalb von Millisekunden. Die Zeitdauer zur Bestimmung eines Standortes besteht jetzt nur noch aus den Beobachtungszeiten. Damit stellt es nun kein großes Problem mehr dar, Standorte in viel kürzeren Zeitabständen hintereinander und viel öfter zu bestimmen – so z. B. mehrmals am Vormittag, mehrmals am Nachmittag oder auch klassisch eine Messung vormittags und eine nachmittags. Das übt auch im Umgang mit dem Sextanten.

3.5 Indexfehler

Jedes Messgerät weist Messfehler auf, so auch Sextanten. Der wichtigste Fehler, der dem Navigator dabei immer begegnet, ist der Indexfehler. Das ist ein sogenannter additiver Fehler oder Offsetfehler. Er verschiebt nur den Nullpunkt auf der Winkelskala. Damit ist er über den gesamten Messbereich konstant und kann einfach durch die Addition eines Korrekturwertes kompensiert werden. Dieser Korrekturwert, die Indexkorrektur, ist nichts anderes als der negative Wert des Indexfehlers. Es muss also nur der Indexfehler durch eine Messung festgestellt werden.
Dies geschieht einfach dadurch, dass man Alhidade und Trommel auf 0° 00’ stellt und dann den Horizont beobachtet. Dabei kann das schwächste farbige Indexschattenglas eingeschwenkt werden. Bei vorhandenem Indexfehler sind jetzt zwei Horizontlinien sichtbar. Diese sind mit der Trommel auf Deckungsgleichheit zu bringen. Der dann ablesbare Winkel ist der Indexfehler und er kann positiv oder negativ sein. Die davon abgeleitete Indexkorrektur ist der gleiche Wert, nur mit entgegengesetzten Vorzeichen.
Der Indexfehler bleibt gewöhnlich über einen längeren Zeitraum konstant und muss in der Berechnung der beobachteten Höhe berücksichtigt werden. Es empfiehlt sich eine monatliche Kontrolle, denn durch Temperaturänderungen, ungewollte Stöße usw. kann er sich verändern. Bei der Verwendung von Plastiksextanten sollte der Indexfehler nach jeder Höhenmessung neu festgestellt werden, denn Plastiksextanten sind bedeutend temperaturempfindlicher als Metallrahmensextanten.
Es gibt allerdings auch Sextanten, die über ein zusätzliches Einstellrad an der Trommel verfügen, mit dem der Indexfehler auf null gestellt werden kann. In dem Fall muss er rechnerisch natürlich nicht mehr berücksichtigt werden.

3.6 Beschickung

Der am Sextanten abgelesene Wert ist nicht der Kimmabstand bzw. die beobachtete Höhe. Diese erhält man erst durch die Addition mit Korrekturwerten. Die gerade behandelte Indexkorrektur ist nur eine davon. Es existieren aber noch mehr Einflüsse, die zu korrigieren sind und auf folgenden Tatsachen beruhen:

1. Ein zu messender Kimmabstand bezieht sich auf die Mitte der Sonne. Die hat dort aber keine Markierung. Deshalb wird bei der Messung in der Regel der Winkel zwischen Kimm und Sonnenunterrand gemessen. Der fehlende Winkel bis zur Sonnenmitte von im Mittel 16’ muss als Korrekturwert hinzuaddiert werden. Wird die Höhe am Oberrand der Sonne gemessen, weil z. B. der Unterrand gerade von Wolken verdeckt ist, dann muss der Winkel bis zur Sonnenmitte subtrahiert werden.
2. Lichtstrahlen werden beim Eintritt in die Erdatmosphäre gebrochen (Refraktion). Der dadurch entstehende Brechungsfehler ist davon abhängig, in welchem Winkel die Lichtstrahlen der Himmelskörper in die Atmosphäre einfallen. Die Dichte der Luft wirkt sich dabei auf das Ausmaß der Refraktion aus. Die Dichte wird vor allem von Luftdruck und -temperatur beeinflusst, die in verschiedenen Höhen und abhängig von Klimazonen und Jahreszeiten unterschiedlich verteilt sind. Der durch Lichtbrechung entstehende Winkelfehler muss korrigiert werden. Ein Problem dabei ist, dass die Refraktion nur näherungsweise zu berechnen ist. Da der Kimmabstand eines Gestirns aufgrund der Refraktion zu hoch gemessen wird, muss ein berechneter Korrekturwert davon subtrahiert werden. Die Gesamtbeschickungstabellen wie z. B. im Anhang unter 8.1 berücksichtigen die Refraktion.
3. Beim Messen steht man auf einem Schiff und je höher der Standort ist, desto weiter kann man über die Rundung der Erdkugel hinweg blicken. Die sichtbare Kimm liegt also mit steigender Standhöhe immer weiter und tiefer. Der mit dem Sextanten feststellbare Kimmabstand der Sonne steigt demnach mit der Höhe, von der aus die Beobachtung vorgenommen wird. Dieser Winkelfehler wird als Kimmtiefe bezeichnet. Diese wird in Gesamtbeschickungstabellen als Augeshöhe berücksichtigt. Auf dem Deck stehend ist sie die Summe von Freibordhöhe des Bootes und Körpergröße. Eigentlich immer, aber besonders bei hoher Dünung, sollte eine Beobachtung deshalb möglichst auf einem Wellenkamm abgeschlossen werden.
4. Die Sonnenscheibe erscheint größer, wenn auf der Nordhalbkugel Winter ist. Das liegt an der elliptischen Bahn der Erde um die Sonne. Dieser Effekt wird mit einer sogenannten Zusatzbeschickung korrigiert.

Zur Berechnung all dieser Einflüsse gibt es Formeln. Die Berechnung des Einflusses der Augeshöhe auf die Kimmtiefe ist dabei sogar recht einfach. Dahingegen ist die genaue Berechnung des Einflusses der Refraktion unmöglich. Neben Formeln für die Refraktion und die Kimmtiefe existieren auch verschiedene Apps. Einfacher und an die Praxis mehr angepasst dürften deshalb Tabellenwerte sein, die in mehr als 100 Jahren erfolgreicher Seefahrt zur Anwendung gekommen sind. Die Nutzung einer Formel zur Berechnung des Refraktionsfehlers, die eine Temperatureingabe verlangt, kann schon stutzig machen, wenn man weiß, dass das Licht durch verschiedene Klimazonen zum Standort kommt, die alle unterschiedliche Drücke und verschiedene Temperaturen aufweisen.

Die Gesamtbeschickungstabelle, die seit Langem im Nautischen Jahrbuch abgedruckt wurde, ist für die Augeshöhe in Zwei-Meter-Schritten bis 40 m gestaffelt und damit für die Großschifffahrt ausgelegt. Sie ist für den Gebrauch auf Segelbooten viel zu grob gehalten. Deshalb wurde nach einer anderen Tabelle gesucht. Im U-Boot-Archiv konnte dann eine solche gefunden werden, die eine Staffelung der Augeshöhe in Ein-Meter-Schritten ausweist, die sich genauer interpolieren lassen – klar, die Brücke von U-Booten ist ja nicht so hoch. Diese Tabelle aus dem Jahr 1935 stimmt in ihren Zwei-Meter-Werten mit den heutigen BSH-Tabellen im Nautischen Jahrbuch immer noch exakt überein. Sie dürfte daher schon damals als optimal gegolten haben. Die Tabelle ist im Anhang unter 8.1 zu finden.
Diese Tabelle liegt der im Kapitel 2 vorgestellten App zugrunde. In der App wird die Augeshöhe jedoch in Dezimetern eingegeben. Einem Computer macht es schließlich nichts aus, zwischen den in Metern angegebenen Tabellenwerten automatisch zu interpolieren.

 

3.6.1 Refraktion

Lichtstrahlen verlaufen nicht linear, wenn sie durch Medien mit sich stetig verändernden Dichten gehen. So ist die Atmosphäre für die aus dem Weltall kommenden Lichtstrahlen ein Medium mit größerer Dichte, die zur Erdoberfläche hin auch noch zunimmt. Die dadurch entstehende kontinuierlich stärker werdende Brechung bewirkt, dass wir die Sterne und auch die Sonne am Himmel höher stehen sehen, als sie wirklich sind.

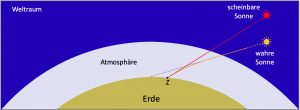
Bild 3.6 soll dies verdeutlichen. Das Licht der wahren Sonne macht beim Eintritt in die Atmosphäre nicht nur einen Knick, wie der Löffel im Wasserglas, sondern neigt sich mit zunehmender Dichte immer stärker in Richtung Erdoberfläche. An unserem Standort Z fallen die Lichtstrahlen daraufhin senkrechter ein als beim Eintritt in die Atmosphäre. Unser Blick geht jedoch tangential zur letzten Einfallskrümmung am Standort nach oben und wir sehen die Sonne in einer höheren Position, aus der in Wirklichkeit überhaupt kein Sonnenlicht kommt. Wir beobachten in diesem Winkel dort also eine Sonne, wo gar keine ist. Die Aufgabe besteht nun darin, auszurechnen, in welchem Maße dieser Effekt Einfluss auf unsere Höhenmessung mit dem Sextanten nimmt. Für die Berechnung der Refraktion findet man verschiedene Formeln, die sich im Wesentlichen nur durch verschiedene Konstanten unterscheiden.Wenn wir physikalisch exakt bleiben wollen, dann brauchen wir ein Modell, um daran eine Gleichung entwickeln zu können. In diesem Fall ist es ein Kugelschalenmodell, das die Erde mit ihrer Atmosphäre im Schnitt sieht. Darin besteht die Atmosphäre aus unendlich vielen Schichten mit nach oben abnehmender Luftdichte. Ein unendliches Summieren geht nur mithilfe der Integralrechnung. In dem folgenden Refraktionsintegral sind n1 bis n∞ die Brechungsindizes unendlich vieler Luftschichten in den Radien r, die vom Erdmittelpunkt aus messen. Gebraucht wird auch der Erdradius selbst, der hier als a eingebracht wurde. Die Brechungsindizes n beinhalten die nach oben abnehmenden Luftdichten infolge von abnehmendem Luftdruck und Temperaturveränderungen. Der scheinbare Zenitabstand ist s. Doch wie diese Abnahme der Luftdichte verläuft, kann niemand genau sagen. Da gibt es Hoch- und Tiefdruckgebiete, die vom Licht durchquert werden müssen, und zudem noch Klimazonen und Jahreszeiten. Wenn man das alles wüsste, dann könnte man die Refraktion auf der Erdoberfläche tatsächlich mit folgendem Integral ausrechnen:

   

Natürlich will niemand mit diesem Integral rechnen. Das Integral kann aber auch in eine unendliche Reihe überführt werden. Bei Kimmabständen über 20° brauchen wir aus dieser Reihe nur die ersten beiden Glieder zu betrachten. Bei kleineren Höhen müssten mehr Glieder berechnet werden. Doch bei kleineren Höhen steigt auch wieder die Unsicherheit. Für Temperatur und Luftdruck, woraus die Dichte folgt, wird ein mittlerer Wert verwendet, der sich in einer Konstanten abbildet. Die Gleichung ist dann bemerkenswert einfach:

(3.1)  

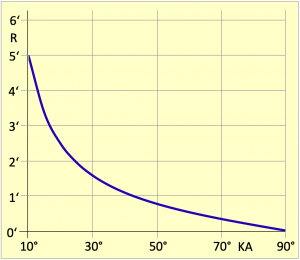
Den Verlauf der Refraktion nach dieser Formel zeigt Bild 3.7. Dort ist sie allerdings bis 10° herunter berechnet. Die Genauigkeit der Ergebnisse eines Kimmabstandes von weniger als 20° ist in diesem Diagramm deshalb nicht garantiert. Überhaupt sollten Gestirne – und das gilt allgemein – nur in Höhen >20° beobachtet werden. Darunter durchqueren die Lichtstrahlen allzu viele Zonen mit unterschiedlicher Luftdichte.

Die Zahlen in der Null-Meter-Spalte der im Anhang befindlichen Beschickungstabelle berücksichtigen keine Kimmtiefe, sind also zum Vergleich mit den Rechenergebnissen der Gleichung 3.1 geeignet. Dabei kann ab einer gemessenen Höhe von 20° eine gute Übereinstimmung festgestellt werden. Bei diesem Vergleich muss lediglich beachtet werden, dass die in dieser Spalte angegebene Zahl die Differenz von 16′ – R ist, wobei 16′ die Hälfte des mittleren Durchmessers der Sonnenscheibe ist.
Dieser mittlere Durchmesser der Sonnenscheibe, der sich im Jahresverlauf ändert, wird in Tafeln mit einer sogenannten Zusatzbeschickung berücksichtigt. Dafür existieren zwei Tabellen im Anschluss an die Beschickungstabelle. Die erste gilt für Messungen am Sonnenunterrand und die darauffolgende für Messungen am Sonnenoberrand.

3.6.2 Kimmtiefe

Die vertikale Distanz zwischen der Achse des Teleskops und der Wasseroberfläche ist die sogenannte Augeshöhe. Auch sie nimmt Einfluss auf den mit einem Sextanten gemessenen Kimmabstand. Der dabei zu betrachtende Einflußparameter ist die sogenannte Kimmtiefe.

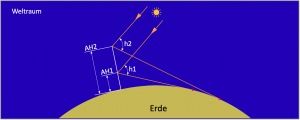
Ihr Einfluss ist im Bild 3.8 gut zu erkennen. Je höher ein Beobachter steht, desto weiter und tiefer liegt die von ihm gesehene Kimm. Die in Bezug zum Horizont im gleichen Winkel einfallenden Strahlen der Sonne werden bei größerer Augeshöhe AH in einem größeren Kimmabstand gemessen (h1 < h2). Zwar ist in dem Bild alles etwas übertrieben groß dargestellt, was aber nur zum besseren Verständnis der Zusammenhänge gemacht wurde. Wer nicht glaubt, dass ein paar Meter Augeshöhe bereits Einfluss nehmen, der beobachte an einem Binnensee im Herbst und im flachen Wasser stehend den Schilfgürtel auf dem nur ein paar hundert Meter gegenüberliegenden Ufer. Das Schilf ist unten schon bis auf etwa 30 cm braun und darüber noch grün. Nun setze man sich hin oder gehe tiefer in Wasser. Dann sieht man den braunen Sockel des Schilfgürtels schon nicht mehr. Daran ist bereits erkennbar, dass die Erde keine Scheibe ist und ihre Rundung bei Messungen immer eine Rolle spielen sollte.
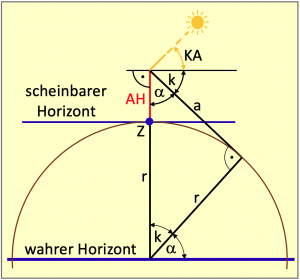
Kommen wir nun zur Berechnung der Kimmtiefe, die wir von einem zu groß gemessenen Kimmabstand abziehen müssen. Bild 3.9 zeigt dazu einen Querschnitt der Verhältnisse – auch wieder sehr übertrieben, aber nur so lassen sich die Dinge anschaulich erklären. Ein Beobachter im Standort Z sieht die Kimm von seiner Augeshöhe AH aus durch das Teleskop seines Sextanten in einer Entfernung von a und gleichzeitig die Höhe der Sonne in einem Kimmabstand von KA + k, wobei k die Kimmtiefe ist, die den wahren Kimmabstand, der zum scheinbaren Horizont gesehen werden muss, verfälscht.
Um k ausrechnen zu können, betrachten wir das Dreieck mit den Seiten (r + AH), a und r. Die Seite a verläuft tangential zur Erdkugel und steht dort, wo sie die Kreislinie berührt, senkrecht zum Radius. Damit handelt es sich um ein rechtwinkliges Dreieck. Wir sehen weiter, dass die Winkel k und α als Stufenwinkel im Erdmittelpunkt wieder erscheinen. Der Kosinus von k ist der Quotient von Ankathete r und Hypotenuse, die aus den beiden Strecken r + AH zusammensetzt. Aus dem Kosinus eines Winkels bekommt man den Winkel selbst über die Arkuskosinusfunktion. Es gilt also:

   

Das ist aber noch nicht alles. Das Ergebnis liegt nämlich im Bogenmaß vor. Zur Umrechnung ins Gradmaß ist eine Multiplikation mit 180 nötig. Eine weitere Multiplikation mit 60 wandelt dann Grad in Bogenminuten um.
Da Lichtstrahlen um 13% mehr gekrümmt sind als die Erdkrümmung (terrestrische Refraktion), wird sogar eine noch weiter entfernt liegende Kimm beobachtet. Die wahre Kimmtiefe beträgt nämlich nur 12/13 des mit der Formel ausgerechneten Wertes. Die endgültige Gleichung lautet aus diesem Grund:

(3.2)  

Manchmal sind auch andere Formeln zu finden. Beispielsweise gibt Joachim Schult in seinem Seglerlexikon k = 1,777-mal Wurzel aus Augeshöhe an. Ob das eine Faustformel ist oder nur aus einer anderen Berechnungsweise stammt, wollen wir jetzt untersuchen. In einem rechtwinkligen Dreieck kann anstelle der Kreisfunktionen auch der Pythagoras zur Anwendung kommen und dann gilt auch:

   

Der erste binomische Lehrsatz verändert den Klammerausdruck und es folgt:

   

Angesichts des großen Erdradius von r = 6.367.707 Metern spielt das Quadrat der Augeshöhe, die wir mit maximal 6 m ansetzen wollen, keine Rolle. Da sich die Quadrate der Erdradien aufheben, erhalten wir nun:

   

   

   

Der Betrag 3568 m wird in nautische Meilen umgerechnet, indem er durch 1852 geteilt wird und wir schreiben dann

   

Unter Berücksichtigung der terrestrischen Refraktion muss noch eine Multiplikation mit 12/13 durchgeführt werden.
Schließlich gilt:

   

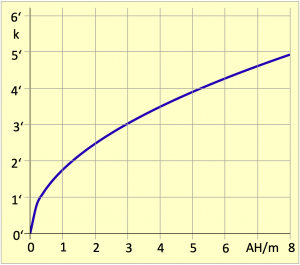
Der Winkel k im Erdmittelpunkt spannt auf der Erdoberfläche die sphärische Distanz mit einer Bogenlänge von ebenfalls k auf und das ist genau der Bogen vom rechten Winkel des Dreiecks bis zum Standort Z. Diese wird mit der Distanz a gleichgesetzt. Die Formel von Joachim Schult ist also plausibel und korrekt. Den Verlauf der Kimmtiefe in Abhängigkeit von der Augeshöhe zeigt das Diagramm im Bild 3.10.
Es sind also schon recht viele Aspekte, die es zu berücksichtigen gilt. Die Summe aller Einflüsse von einem halben Sonnendurchmesser, Kimmtiefe und Refraktion sind als Gesamtbeschickung in den Nautischen Jahrbüchern des BSH in mehreren Tabellen abgedruckt worden und auch Teil des Anhangs.

 

3.7 Hinweise zum Kauf eines Sextanten

Das Angebot an gebrauchten Sextanten im Internet ist riesig. Darunter befindet sich bestimmt auch eine ganze Menge brauchbarer Instrumente. Zum überwiegenden Teil dürften dies allerdings Ziersextanten und somit Dekorationsstücke für die heimische Vitrine sein. Vor allem bei den angebotenen Messingsextanten könnte es sich um den Nachbau antiker oder klassischer Modelle handeln, die nicht an Bord eines Schiffes gehören. Wer einen Sextantenkauf plant, der sollte sich vorher gut informieren, um Fehlkäufe zu vermeiden.
Es ist schwer, den Unterschied zwischen einem Ziersextanten und einem echten Navigationsinstrument auf einem Foto zu erkennen. Das gelingt nicht einmal einem Profi. Selbst wenn man auf einem Bild ein bekanntes Modell erkennen kann, dann ist noch lange nicht gesagt, dass gerade dieses Instrument in Ordnung ist oder gar einen versteckten Fehler aufweist. Die Wahrheit stellt sich immer erst nach einer etwas längeren Nutzung heraus.

So vertraute ich nie irgendwelchen Angeboten im Internet oder auf Flohmärkten, obwohl man die Stücke dort sogar in die Hand nehmen konnte. Man sollte bedenken, dass Sextanten mit einer Genauigkeit von 1/1000 mm gefertigt werden, und das hat sicherlich Gründe.
Vielleicht kommt man heute sogar an Marinesextanten heran, die bis vor kurzem noch auf Berufsschiffen ausrüstungspflichtig waren und nun irgedwo herumliegen, weil sie nicht mehr gebraucht werden. Es gibt allerdings auch genügend Kapitäne, die diese Stücke behalten wollen.
Wichtig ist der Zweck, für den ein Sextant angeschafft werden soll. Wenn dieser nur in einem Notfall zur Anwendung kommen soll, dann reicht ein billiger Plastiksextant. Sogenannte Übungssextanten gibt es schon ab 60 Euro. Diese kann man natürlich nicht für eine ernsthafte Navigation gebrauchen. Sie würden es aber ermöglichen, nach Hause zurückzufinden: eine Notfallnavigation also. So ein Plastiksextant findet außerdem auf jeder Yacht einen Platz.
Wer allerdings ernsthaft Astronavigation betreiben möchte, wird sich mit einem Übungssextanten nicht zufriedengeben wollen. Es gibt aber auch Vollsicht-Plastiksextanten, die das erlauben. Störend wird hier der stark temperaturabhängige Indexfehler sein, denn dieser sollte nach jeder Höhenmessung neu festgestellt werden. Wird das sorgfältig gemacht, dann kann mit diesen Sextanten ein Standort fast so genau bestimmt werden wie mit vielen Typen von Metallsextanten. Ein großer Vorteil von Plastiksextanten ist deren geringes Gewicht. Damit können dann auch zartere Frauen gut umgehen. Ein weiterer Vorteil ist eine gewisse Robustheit, die grundsätzlich allen Plastikartikeln zugesprochen werden kann.
Man sollte das Hobby Astronavigation jedoch nicht gleich mit sehr teuren Instrumenten beginnen. Für Anfänger gut geeignet sind Vollsicht-Plastiksextanten, die neu etwas mehr als 300 € kosten. Wenn das Hobby ausgeweitet werden soll, kann man sich immer noch ein hochwertiges Instrument zulegen. Ich selbst hatte mir vor Jahren, ich glaube es war im Jahr 2007, einen Edelstahl Sailing-Sextanten des Typs GLH 130-40 für etwa 500 € gekauft. Dies war ein chinesischer Nachbau des einstigen Standardsextanten cass 41400. Dieser erfüllt seinen Zweck noch heute. Allerdings ist er in Deutschland nicht mehr im Handel. Verschiedene Händler, u. a. ALIBABA, bieten ihn aber weiterhin im stabilen Holzkasten für jetzt 300 € an.
Später hat mich dann auch einmal interessiert, wie gut der Plastiksextant Mark 25 zu gebrauchen ist. Ich war sogar angenehm überrascht. Sowohl hinsichtlich seiner Handhabung als auch Präzision machte er keinen schlechten Eindruck. Man sollte nur etwas Vaseline auftragen, damit die Alhidade besser gleitet.
Auf meinem Boot besitze ich auch das Spitzenmodell des Herstellers Cassens & Plath, einen HORIZON ULTRA. Dieser wird allerdings nur an „Sonntagen“ benutzt und ist sonst mehr ein Statussymbol auf meiner Yacht. Das „Arbeitstier“ ist nach wie vor mein alter Marinesextant GLH 130-40.
Die Spitzenmodelle haben natürlich ihren Preis, der zwischen 1000 € für einen einfachen Sailing Sextanten und mehr als 2000 € für einen professionellen Sextanten liegt. Im Bild 3.11 ist ein hochwertiger Sextant abgebildet, der eine Kompensationsmöglichkeit für seinen Indexfehler aufweist. Das Modell trägt den Namen des bekannten Weltumseglers Bobby Schenk, auf den diese zusätzliche Kompensationsmöglichkeit zurückgeht. Diese Indexschraube besitzt mein Horizon Ultra ebenfalls.