4 Analytische Positions-Bestimmung

Links → Kapitel 1, Kapitel 2, Kapitel 3, Kapitel 5 und 6, Kapitel 7, Kapitel 8

Der bedeutendste deutsche Navigationslehrer Friedrich August Arthur Breusing (1818–1892) war kein Freund grafischer Navigationsmethoden und lehnte deshalb das Sumner-Verfahren ab. In seinem Lehrbuch „Steuermannskunst“, das als Standardwerk der Hochseenavigation in vielen Auflagen noch nach seinem Tod bis weit ins 20. Jahrhundert hinein erschien, nahm er das Verfahren von Saint Hilaire erst in einer späteren Auflage auf.
Bemerkenswert ist, dass die Gauß-Methode in keiner der zehn Auflagen seines Lehrbuches auch nur erwähnt wurde. Es ist kaum anzunehmen, dass Breusing als Direktor der damals führenden deutschen Navigationsschule, die die Steuermannsschule in Bremen war, von der Gauß-Methode nichts wusste. Dabei ist gerade dieses Verfahren das brillianteste analytische Stück der Lösung des Zweihöhenproblems überhaupt.
Strenge analytische Methoden, obwohl sie im Gegensatz zu den grafischen Näherungsmethoden mathematisch exakt waren, konnten zu seinen Zeiten nicht angewendet werden, weil es keine Computer gab. Trotz des Umsichgreifens der neuen grafischen Methoden, die das Bestreben hatten, alles Alte zu verdrängen, nahm er in der 5. Auflage seines Lehrbuches die Methode von Borda und Lalande noch auf. Das Verfahren von Borda ist zwar keine streng analytische Methode, sondern eine Iterationsmethode, aber sie ist nicht grafisch.
Im Weiteren wollen wir uns mit den mathematisch exakten Verfahren auseinandersetzen. Dabei kommen wir um den Gebrauch der sphärischen Trigonometrie nicht herum. Diese ist aber einfacher, als mancher denken mag. Daher wollen wir uns erst einmal einigen Dingen der Kugelgeometrie zuwenden.

4.1 Ein bisschen Mathe

Sie sollten nun bitte keinen Schreck bekommen – ich weiß, dass Mathematik für viele ein Unwort ist. Wenn Mathematik aber gut dargeboten wird, kann sie viele Menschen sogar begeistern und wird kaum noch jemanden abschrecken. Wir wollen sie im Nachfolgenden auch so darbieten, dass jeder sie verstehen kann. Der französische Mathematiker und Philosoph Jean-Baptist le Rond d’Alembert hatte folgende Meinung über die Mathematik:

„Die Mathematik ist eine Art Spielzeug, welches die Natur uns zuwarf zum Troste und zur Unterhaltung in der Finsternis.“

Tatsächlich genügt zum umfassenden Verständnis sämtlicher Methoden der Astronavigation, ob es die von Borda, Sumner, Hilaire oder anderer sind, eine einzige Formel und diese ist nicht einmal kompliziert. Sie wird nur immer kompliziert dargeboten, so als ob manche Autoren zeigen wollen würden, was sie so können. Dies möchten wir hier tunlichst vermeiden. Die Formel heißt Kosinus Seitensatz und wird dazu verwendet, in einem Dreieck auf der Oberfläche einer Kugel entweder eine Seite oder einen Winkel auszurechnen.
Wir betrachten zunächst einmal das Bild 4.1 auf der linken Seite. Es zeigt eine Kugel, deren Oberfläche von drei Großkreisen mit demselben Durchmesser der Kugel überzogen ist. Die drei Kreislinien beranden auf der Kugeloberfläche insgesamt acht mögliche Dreiecke verschiedener Größe, von denen wir uns aber nur eines der beiden kleineren genauer ansehen wollen.
Wie in der Geometrie der Ebene sind die Ecken mit den Großbuchstaben ABC, die Seiten mit den Kleinbuchstaben abc und die Winkel zwischen den Seiten mit den griechischen Buchstaben α β γ gekennzeichnet. Einen wesentlichen Unterschied zu einem Dreieck in der Ebene werden wir gleich feststellen. Während man Seitenlängen eines Dreiecks in der Ebene in Zentimetern, Metern oder Meilen misst, werden die Seitenlängen eines Kugeldreiecks in Grad gemessen.

Wie es dazu kommt, sieht man im Bild 4.1 auf der rechten Seite. Ein Winkel b im Kugelzentrum spannt auf der Kugeloberfläche einen Kreisbogen mit einer Länge von b auf. Die Bogenlänge wird primär jedoch nicht in Metern, Zoll oder irgendeinem anderen Längenmaß gemessen, sondern im selben Gradmaß wie der Winkel b im Erdinnern. Die Länge des Bogens b ist das sogenannte Bogenmaß des Winkels b im Zentrum der Kugel. Beide werden in Grad gemessen und besitzen dieselbe Gradzahl.

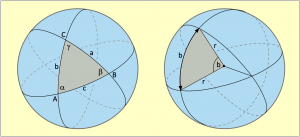
Damit ist in der sphärischen Trigonometrie alles relativ. Ob die Seite eines Kugeldreiecks auf einer Murmel oder auf der Erdkugel betrachtet wird, spielt erstmal keine Rolle. Wenn ein ausgerechneter Bogen eine Länge von 3 Grad besitzt, dann sind dies auf der Erdkugel 180 abzuschreitende Seemeilen und auf der Murmel nicht mal ein Millimeter. Doch genau das macht die sphärische Trigonometrie manchmal so einfach und auch so interessant.
Wir stellen fest, dass hier ausschließlich Kreise im Spiel sind. Winkel in den Kreismittelpunkten sind allerdings auch nötig, um Kreisbögen definieren zu können, wie es Bild 4.1 rechts mit dem Winkel b und dem Kreisbogen b aufzeigt. Aus diesem Grund werden in Berechnungen alle verwendeten Seiten und Winkel in Kreisfunktionen verwendet. Kreisfunktionen sind die Sinus- und die Kosinusfunktion.
Warum das so sein muss, soll an dieser Stelle nicht weiter vertieft werden. Daraus folgt, wenn wir aus den Seiten a, c und dem Winkel β eines sphärischen Dreiecks die Seite b ausrechnen wollen, dann können wir das nur mit den Kreisfunktionen dieser drei Elemente umsetzen. Wir rechnen also nicht mit der Seite a, sondern mit cos(a) oder sin(a). Für die Seite c gilt dann cos(c) oder sin(c) und anstelle des Winkels β benutzen wir cos(β) oder sin(β). Ob gerade der Kosinus oder der Sinus zu gebrauchen ist, zeigen die Regeln des Kosinus Seitensatzes weiter unten. Die Art und Weise, wie diese Formel einst hergeleitet wurde, lassen wir mal außen vor. Natürlich bekommen wir als Ergebnis keine Seite und auch keinen Winkel geliefert, sondern ebenfalls immer nur den Kosinus oder Sinus einer Seite oder eines Winkels in einer Kreisfunktion.
Doch wie kommt man am Ende von cos(b) wieder auf b oder von sin(β) auf β Das geht ganz einfach mit der Umkehrfunktion, die sich Arkusfunktion (lat. arcus = Bogen) nennt und äußerst einfach zu handhaben ist.
Wenn wir eine Seite ausrechnen wollen, beispielsweise die Seite b, aber nur eine Formel haben, um cos(b) ausrechnen zu können, dann stellt das kein Problem dar. Wir ersetzen den Kosinus durch den Arkuskosinus. Dazu hier ein Beispiel: Wenn wir

   

haben, aber b ausrechnen wollen, dann schreiben wir die Formel einfach um und erhalten

   

Die Klammern um die Argumente lassen wir künftig weg. Wir werden also sin anstelle von sin() schreiben und anstatt arccos kann auch cos^-1 geschrieben werden. Diese Schreibweise findet vor allem auf Taschenrechnern Anwendung. Haben wir dort für cos b die Zahl 0,9993908 im Display stehen, dann können wir auf vielen Modellen einfach die Taste cos^-1 drücken. Im Display steht dann die Zahl 2, was dann 2° sind.

4.1.1 Der Kosinus Seitensatz

Der Kosinus Seitensatz wird in zwei Varianten benutzt. Die erste Variante wird verwendet, wenn eine Dreieckseite berechnet werden soll. Dazu müssen die beiden anderen Seiten und der Winkel zwischen diesen Seiten bekannt sein. Um die Seite b im Bild 4.2 berechnen zu können, benötigt man also die Seiten s und p sowie den davon eingeschlossenen Winkel ψ (psi).
Die Berechnungsformel dafür lautet:

   

Oder als Regel 1 in Worten:

Der Kosinus einer Seite ist gleich dem Produkt der Kosinusse der anderen beiden Seiten vermehrt um das mit dem Kosinus des Zwischenwinkels multiplizierte Produkt der Sinusse dieser beiden Seiten.

Will man einen Winkel berechnen, dann müssen alle Seiten bekannt sein. Zur Berechnung des Winkels im Bild 4.2 muss die folgende Formel angewendet werden:

   

Oder als Regel 2 in Worten:

Der Kosinus eines Winkels ist gleich dem Kosinus der dem Winkel gegenüber liegenden Seite, vermindert um das Produkt der Kosinusse der übrigen Seiten, geteilt durch das Produkt der Sinusse der übrigen Seiten.

Im Prinzip ist das schon die ganze sphärische Trigonometrie, wie sie in der Astronavigation gebraucht wird. Man muss jetzt nur noch die Größen b, p und s definieren, denn diese kennen wir noch nicht. Wir kennen nur die Breite als geschätzte Breite oder Koppelbreite, weiterhin die Deklination δ und den mit einem Sextanten gemessenen Horizontabstand h.
An dieser Stelle kommen die Komplementbeziehungen als Vereinfachungen ins Spiel. Ein Komplementwinkel oder einfach das Komplement eines Winkels ist seine Ergänzung zu 90°. Hat ein Winkel einen Betrag von 60°, dann beträgt sein Komplementwinkel 30°. Weil die Strecke vom Äquator bis zum Pol immer 90° beträgt, ist im Bild 4.2 die Deklination δ das Komplement der Seite p und das Komplement der Seite b auf dem Standortmeridian ist die Breite . Die folgende Tabelle zeigt alle hier geltenden Komplemente.

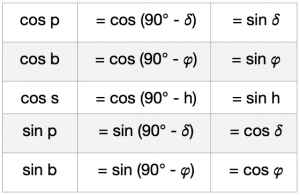
Mit den Komplementen der Seiten bekommen wir überhaupt erst einen Zugriff auf die wahren Seiten. Wir wissen doch gar nicht, wie lang die Seiten b, s oder p sind, um damit ausrechnen zu können. Doch mit den Komplementen, den Ergänzungen zu 90°, fällt das ganz einfach. Anstelle der unbekannten Seite cos p wird die bekannte Deklination sin δ eingesetzt, was absolut dasselbe ist. So vereinfachen sich die Formeln. Ohne diese müssten in den Gleichungen für cos p der Ausdruck cos (90° – δ) und für sin p der Ausdruck sin (90° – δ) eingesetzt werden. Die Folge wären lange Formelausdrücke. Die Tabelle zeigt in der ersten Spalte die Seiten und in der dritten Spalte die Komplemente der Seiten.
Unter Benutzung der Komplemente tauschen wir dann alles aus und erhalten die neue Formel zur Berechnung der Seite b:

   

Wir könnten jetzt über die Arkuskosinusfunktion das Bogenmaß der Seite b ausrechnen, dieses von 90° subtrahieren und hätten die Breite  Es geht aber noch einfacher. Die Komplemente in der Tabelle zeigen, dass cos b dasselbe ist wie sin  Deshalb benutzen wir anstelle von arccos gleich arcsin und haben die Breite direkt, wie die nachstehende Formel zeigt:

(4.1)  

Anstelle von arcsin kann auch sin^-1 geschrieben werden.
In der zweiten Formel zur Berechnung des Polwinkels tauschen wir die Elemente s, p und b gegen die Komplemente h, δ und und bekommen:

   

Den Polwinkel selbst bekommen wir hier mit der Arkuskosinusfunktion:

(4.2)  

Wie aber erklären sich die Komplementbeziehungen? Das liegt am Verlauf der Kreisfunktionen Sinus und Kosinus, die im Bild 4.3 über eine Schwingungsperiode zu sehen sind. Der Verlauf der Kurven setzt sich ins Positive und ins Negative unendlich weit fort. Die Amplitude schwankt dabei nur zwischen +1 und -1. Deutlich erkennbar ist der Phasenunterschied in den Verläufen beider Kurven, der genau 90° beträgt. Der Funktionswert 1 oder 0 beider Kurven unterscheidet sich um 90°. Hat die Kosinuskurve den Wert 1, dann hat ihn die Sinuskurve 90° danach oder davor. Dies trifft nicht nur auf 0 und 1 zu, sondern alle Funktionswerte der beiden Kreisfunktionen unterscheiden sich permanent um 90°.

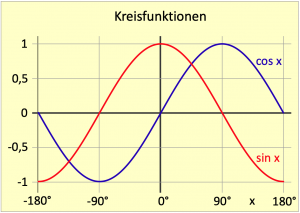
Weitere wichtige Eigenschaften bestehen darin, dass die Kosinuskurve symmetrisch zur Nullachse liegt. Daraus folgt, dass Funktionswerte positiver und gleichnamiger negativer Winkel identisch sind. Es gilt cos(+x) = cos(-x). Bei der Sinuskurve gilt, dass die Funktionswerte von gleichnamigen positiven und negativen Winkeln ein umgekehrtes Vorzeichen besitzen, also sin(+x) = – sin(-x).

Das ist jetzt aber wirklich die ganze Mathematik, die ausreicht um alle bekannten klassischen Methoden der astronomischen Navigation zu beschreiben und zu verstehen und sofern man das will, zu berechnen.
Sollte jemand einmal darauf angewiesen sein, mit dem Sextanten nach Hause finden zu müssen, was durchaus schon passiert ist, dann hilft auch ein Handy nicht lange, weil der Akku nach ein paar Tagen leer geht, wenn kein Solarlader an Bord ist. Es gab auch schon den Fall, dass ein Boot tagelang im Watt festsaß und den Seenotrettern kein Standort mitgeteilt werden konnte, weil beide, Skipper und Mitsegler, ihr Handy vergessen hatten. Ein Sextant, die Gleichung 4.2, ein Nautisches Jahrbuch und eine Armbanduhr könnten hier schon helfen – und natürlich ein Taschenrechner.
Die Breite bekommt man aus der Mittagsbreite. Daraus und aus der ein paar Stunden später gemessenen Sonnenhöhe sowie der Deklination aus dem Nautischen Jahrbuch berechnet man mithilfe der Gleichung 4.2 den Stundenwinkel was schnell auf einem Taschenrechner zusammengetippt ist. Das Nautische Jahrbuch, das man an Bord haben sollte, liefert auch den Grt und wenn der Stundenwinkel davon subtrahiert wird (es ist Nachmittag), hat man die Standortlänge und könnte den Seenotrettern den Standort durchgeben. 
Dies sollte jetzt keine Anleitung für ein einfaches Back-up sein, sondern lediglich zeigen, wie simpel Astronavigation eigentlich ist. Das ist übrigens genau das Verfahren, mit dem James Cook während seiner gesamten zweiten Reise navigierte. Ein Nautisches Jahrbuch hatte er zwar nicht, dafür aber Deklinationstabellen und Zeitgleichungstabellen. Den Grt bzw. GHA bekam er, indem er die Zeitgleichung mit der Differenz von Chronometerzeit und 12:00 GMT addierte und das Ergebnis mit der Winkelgeschwindigkeit der Sonne von 15°/h multiplizierte – ganz schön aufwendig.
Seine Reise begann 1772 und dauerte drei Jahre. Dabei legte er mehr als 300 000 km zurück. Sein Auftrag war die Suche nach der Antarktis, die er jedoch nicht fand und stattdessen die erste und erstaunlich präzise Karte der Südseeinseln herstellte. Als Chronometer stand ihm ein exakter Nachbau der im Bild 1.5 abgebildeten H4 zur Verfügung. Das Original der H4 von John Harrison durfte er nicht mitnehmen, weil es infolge mehrfachen Zerlegens vor der Längengradkommission für diese Reise nicht mehr in Frage kam. Der Londoner Uhrmacher Larcum Kendall fertigte für diesen Zweck nach Harrisons Anweisungen eine exakte Kopie an, die später die Bezeichnung K1 erhielt. James Cook bezeichnete Harrisons Erfindung als „unseren nie versagenden Führer“ oder „unseren zuverlässigen Freund“.
Weil die Breite bei diesem Verfahren immer nur geschätzt wurde, kann sie von der wahren Breite abweichen. Wiederholt man dieselbe Berechnung nur mit einer weiteren Breite, dann erhält man auf dieser zweiten geschätzten Breite eine andere Länge und somit einen zweiten möglichen Standort. Zieht man durch beide mögliche Standorte eine Linie, dann ist das eine Standlinie, denn irgendwo, aber auf dieser Linie wird der Standort des Schiffes sein. Das ist genau die Standlinie, die Kapitän Sumner bei seiner denkwürdigen Reise 1837 entdeckt und damit die Ära der modernen Astronavigation begründet hat.

Mit der Erfindung einer genau gehenden Uhr und einer einzigen einfachen mathematischen Formel brach in der Geschichte der Navigation ein neues Zeitalter an.

Wir sind heute nicht mehr darauf angewiesen, unseren Standort durch manuelles Ausrechnen von Formeln zu finden, es sei denn, wir wollen das. Computer, Smartphones und Tablets übernehmen die Rechenarbeit. Formeln sind nur wichtig zum Begreifen der Materie und dafür, dass Softwareentwickler die entsprechenden Programme für diese Geräte schreiben können. Der Sinn aller Formeln in den hier gezeigten Beiträgen besteht also nur in der exakten Beschreibung der Zusammenhänge und soll keine Anleitung zur praktischen Navigation sein. Außerdem wurde viel Wert darauf gelegt, akademischen Ballast wegzulassen.

 

4.2 Bildpunkt und Höhenkreis

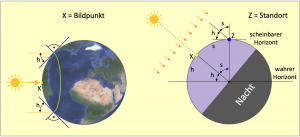
Wir wollen uns jetzt mit zwei Begriffen auseinandersetzen, die für das weitere Verständnis gebraucht werden. Das ist zunächst der Bildpunkt eines Gestirns, so auch der Sonne, und die Frage danach, welche Informationen uns die unterschiedlichen Höhen bzw. senkrechten Abstände von der Horizontlinie geben.
Auf dem flachen Land oder der See sehen wir Turmspitzen oder Berge immer höher, je mehr wir uns ihnen annähern. Aus dem Höhenwinkel und der bekannten Höhe eines Bauwerkes oder eines Berggipfels ließe sich danach ganz einfach die Entfernung berechnen.
Sonne und Sterne sind jedoch unendlich weit weg und ihre tatsächliche Entfernung würde uns auch nicht weiterbringen. Uns hilft es, zu wissen, dass die Erde eine Kugel ist. Dadurch können wir die Entfernung zum irdischen Bildpunkt eines Gestirns trotz seiner riesigen Entfernung bestimmen. Der Bildpunkt ist sozusagen der Fußpunkt des Gestirns auf der Erdoberfläche. Eine ältere Bezeichnung lautet Zenitalpunkt und trifft es vielleicht sogar besser, denn dies ist der Punkt, an dem das Gestirn bzw. die Sonne im Zenit beobachtet wird. In einer geometrischen Betrachtung müsste man die Mittelpunkte von Sonne und Erde mit einer gedachten Linie verbinden. Der Bildpunkt der Sonne ist dann der Ort, an dem diese gedachte Linie die Erdoberfläche durchbricht. Bild 4.4 zeigt dies auf der linken Seite schematisch. Die Position dieses Ortes ist nicht fest, denn die Erde dreht sich und damit rast der Bildpunkt mit Jetgeschwindigkeit in Richtung Westen.
Die Position des Bildpunktes der Sonne wird mit einem Stundenwinkel, dem Grt und der Deklination beschrieben. Diese Positionsdaten werden auch als Ephemeriden bezeichnet. Der Greenwich Stundenwinkel Grt, der im internationalen Sprachgebrauch als GHA bezeichnet wird, zählt vom Nullmeridian nach Westen gehend von 0 bis 360° einmal um die Erde.
Die Deklination ist der Breitengrad des Bildpunktes. Er wechselt zwischen den Sonnenwenden von etwa 23,44° S nach 23,44° N. Ursache der Deklination ist die schrägstehende Erdachse, was den Wechsel der Jahreszeiten bewirkt. Wie das funktioniert, lässt sich ganz gut im Bild 7.3 erkennen.
Im Gegensatz zu einem kartesischen Koordinatensystem sind die Kugelkoordinaten des Gradnetzes der Erde begrenzt zwischen jeweils 90° Nord und 90° Süd bzw. 180° Ost und 180° West. Westlängen und Südbreiten besitzen negative Vorzeichen:

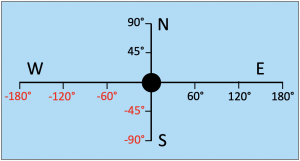
Die Skala von Stundenwinkeln, wie dem Grt oder dem LHA, weicht davon allerdings ab, denn sie zählen erdumlaufend von 0° bis 360°. Wenn in einer Berechnung Stundenwinkel von größer als 360° oder kleiner als null entstehen, dann sind das Überträge und es müssen einfach nur 360° subtrahiert oder 360° addiert werden, womit der Winkel wieder in den zulässigen Zahlenbereich gelangt.
Diese Regel gilt auch bei geografischen Längenangaben, wobei die Überträge schon bei Überschreitung von jeweils 180° entstehen. So sind von einem Überlauf auf 182° E 360° zu subtrahieren und daraus werden dann -178° bzw. 178° W.
Wie Bild 4.4 links erkennen lässt, würden alle Beobachter, die sich gerade auf der grün dargestellten Kreislinie befinden, die Sonne zur selben Zeit in derselben Höhe h sehen. Diese Kreislinie hat deshalb die Bezeichnung Höhengleiche. Sie kann aber auch Höhenkreis genannt werden. Es ist ein Kreis mit einem sphärischen Radius, dessen Länge mit s bezeichnet werden soll.

Wenn also ein Beobachter eines Gestirns immer auf der Höhenkreislinie eines gerade von ihm beobachteten Gestirns steht, dann steht er gleichzeitig auch auf der Höhenkreislinie eines beliebig anderen Gestirns, das er von derselben Stelle aus beobachten kann. Genau darin besteht schließlich das Wesen der astronomischen Navigation. Die Höhenkreise der zwei Gestirne kreuzen sich direkt unter den Füßen des Beobachters, und damit buchstäblich in seinem Standort. Die Aufgabe ist also einfach formuliert:

Einen Standort zu ermitteln heißt, die Schnittpunkte zweier beobachteter Höhenkreise zu bestimmen.

Dasselbe funktioniert auch mit Höhenkreislinien nur eines Gestirns wie der Sonne. Auch dabei kreuzen sich die Höhenkreise im Beobachterstandort, wenn die Sonne in einem zeitlichen Abstand wiederholt beobachtet wird. Auch daraus resultieren zwei oder sogar mehrere unterschiedliche Höhenkreise.
Zur Berechnung eines Standortes muss man die Kreise kennen. Die Positionen ihrer Mittelpunkte findet man anhand der Beobachtungszeit in einem nautischen Almanach. Was dann nur noch fehlt, ist die Länge der Radien, womit wir uns nun kurz befassen wollen.

Der Zusammenhang zwischen der mit einem Sextanten gemessenen Höhe h und der Länge s des sphärischen Radius ist im Bild 4.4 rechts ganz gut zu erkennen. Die beiden Winkel h und s existieren im Standort aber gleichzeitig auch im Erdmittelpunkt. Betrachtet man die Winkel im Erdmittelpunkt, dann sieht man, dass sie auf der Erdoberfläche die Kreisbögen h und s aufspannen, die beide zusammen ein Viertel des Erdumfangs, also 5 400 NM ergeben. Ein Beobachter im Standort Z sieht die Sonne in einer Höhe bzw. in einem Horizontabstand von h. Damit beträgt der Zenitabstand s = 90° – h und wir wissen bereits, dass der Zenitabstand die sphärische Länge des Radius des Höhenkreises der Sonne im Beobachtungszeitpunkt ist. Wird mit einem Sextanten ein Horizontabstand von 40° gemessen, dann beträgt der Zenitabstand 50°. Mit 60 Seemeilen pro Grad ist das eine Radiuslänge von 3 000 nautische Meilen.

 

4.3 Standort direkt aus zwei Höhenkreisen

Diese bereits in 1.1 kurz beschriebene Aufgabe ist sehr alt, konnte jedoch wegen ihres Rechenaufwandes auf See nicht benutzt werden. Zu ihrer Lösung mit Logarithmen hätte man nicht weniger als 24-mal die verschiedenen Logarithmentafeln mit oder ohne Winkelfunktionen aufschlagen müssen, wobei dann auch gleich 24-mal hätte interpoliert werden sollen. Um Rechenfehler möglichst ausschließen zu können, hätte der arme Navigator das Ganze noch einmal wiederholen dürfen. Selbst geübte Rechner würden für diese Arbeit mehr als eine Stunde brauchen.
Ein präzises Ergebnis wäre auch nur bei der Beobachtung von zwei Sternhöhen kurz hintereinander möglich gewesen. Bei einer Standortbestimmung mit der Sonne wird man zwischen den Beobachtungen immer eine Zeit von einigen Stunden warten müssen, in denen das Schiff weitergesegelt wäre. Eine exakte Standortberechnung unter Berücksichtigung dieser Versegelung wäre auch nur durch ein teilweises Wiederholen des Rechenalgorithmus möglich.
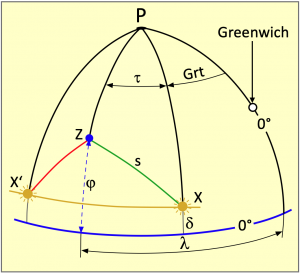
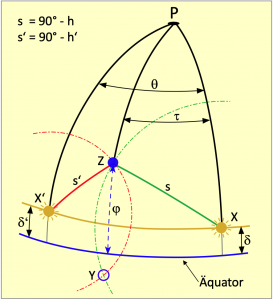
Eine Berechnung des Standortes ist im Grunde eine einfache Geometrieaufgabe. Im Bild 4.5 sind alle Elemente vorhanden, um den Rechenweg gut erklären zu können. Darin sind P der Nordpol, sowie X und X’ die Positionen der Sonne bzw. ihres Bildpunktes in den Zeitpunkten einer ersten und zweiten Beobachtung. Der zentrale Punkt Z ist der Zenit eines Beobachters und damit der Standort eines Schiffes.
Diese vier Punkte bilden insgesamt vier Kugeldreiecke aus. Das große Dreieck XPX’ umrandet drei kleinere Dreiecke, bestehend aus den beiden Polardreiecken XPZ und X’PZ, gebildet aus einer ersten und einer späteren zweiten Beobachtung der Sonne. Schließlich gibt es noch das dritte zentrale Dreieck XZX’.

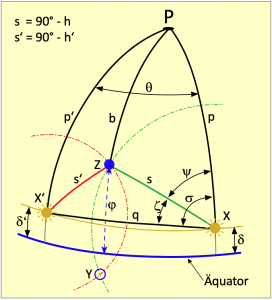
Alle Dreiecke werden von Großkreisbögen umrandet. So enden die Winkel ζ und σ nicht auf der in orange dargestellten Deklinationslinie, denn das ist kein Großkreis. Sie enden auf dem Großkreisbogen q, der kürzesten Verbindung zwischen den Sonnenbildpunkten X und X’. Bei den Seiten s und s’ handelt es sich um die Komplemente der jeweils beobachteten Höhen der Sonne, denn es gilt s = 90° – h und s’ = 90° – h’. Dass es dabei ebenfalls um Großkreisbögen geht, ist einfach zu beweisen. Der kürzeste Abstand zwischen zwei Punkten auf einer Kugel folgt bekanntlich einer Großkreislinie. Eine direkte Sichtverbindung zu einem Gestirn folgt ebenfalls einer kürzesten Verbindung und diese Sichtlinie liegt deckungsgleich senkrecht über dem Großkreisbogen. Die Seiten p, p’ und b folgen Meridianen und sind damit sowieso Großkreisbögen. Die Seite b ist eine gemeinsame Seite der beiden Polardreiecke und das Komplement der Standortbreite  Die Aufgabe besteht zunächst darin, die Bogenlänge der Seite b zu berechnen.

 

4.3.1 Berechnung der Breite

Die Berechnung ist allein mit dem Kosinus Seitensatz schnell erledigt. Wir erinnern uns an seine beiden Verwendungsmöglichkeiten:

1. Der Kosinus einer Seite ist gleich dem Produkt der Kosinusse der anderen beiden Seiten vermehrt um das mit dem Kosinus des Zwischenwinkels multiplizierte Produkt der Sinusse dieser beiden Seiten.
2. Der Kosinus eines Winkels ist gleich dem Kosinus der dem Winkel gegenüber liegenden Seite, vermindert um das Produkt der Kosinusse der übrigen Seiten, geteilt durch das Produkt der Sinusse der übrigen Seiten.

Daraus ergibt sich nun der folgende fünf Punkte Plan:

1. Nach A. wird mit den Seiten p und p’ des umfassenden Dreiecks und dem davon eingeschlossenen Winkel θ die Seite q berechnet.
2. Danach sind von dem großen Dreieck alle Seiten bekannt und der Winkel σ wird nach B. bestimmt.
3. Da gleichfalls alle Seiten des zentralen inneren Dreiecks bekannt sind, wird in derselben Weise nach B. auch der Winkel bestimmt.
4. Aus der Winkeldifferenz ψ = σ – ζ erhält man den Zwischenwinkel der Seiten s und p.
5. Da die Seiten s und p bekannt sind und nun auch der davon eingeschlossene Winkel , kann die Seite b berechnet werden, oder besser gleich das Komplement  dieser Seite.

Das Ganze ist also recht übersichtlich und wir wollen den Plan auch gleich formeltechnisch umsetzen. Gebraucht wird dazu lediglich der Kosinus Seitensatz.

1) Gemäß A. gilt für die Grundseite des umfassenden Dreiecks die Gleichung:

   

Nach Ersetzten aller Variablen mit ihren Komplementen gem. Tafel 4.1 folgt daraus

   

und schließlich:

(4.3)  

2) Die Berechnung des Winkels σ erfolgt unter Anwendung von B.:

   

.Nach Ersetzen der Variablen mit den Komplementen folgt daraus:

   

und schließlich:

(4.4)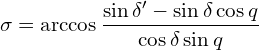  

3) Was im großen Dreieck die Seiten δ und δ’ darstellen machen im kleinen zentralen Dreieck die Seiten h und h’ aus. Die Formel zur Berechnung des Winkels ζ ist also dieselbe wie Gl. 4.4, nur dass δ und δ’ gegen h und h’ getauscht werden müssen und wir schreiben:

(4.5)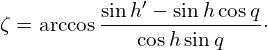  

4) Um gemäß A. die Seite b berechnen zu können, muss der Winkel zwischen den Seiten p und s bekannt sein. Dieser ist die Differenz

(4.6)  

5) Die Seite b ist das Komplement der Breite ψ. Man könnte also formal b berechnen und von 90° abziehen, woraus die Breite folgt. Besser ist es jedoch, anstelle von b das Komplement von b, nämlich gleich die Breite  zu berechnen. Dazu muss dann aber die Arcussinusfunktion angewendet werden. Wir schreiben deshalb:

(4.7)  

Bild 4.5 zeigt, dass sich die Höhenkreise mit den Radien s und s’ an zwei möglichen Stellen schneiden und somit auch ein Standort Y südlich der Deklinationsbreite möglich ist. Dieser ist immer dann zu berechnen, wenn die Mittagssonne in der nördlichen Hemisphäre beobachtet wird.
Soll der südliche Schnittpunkt der Höhenkreise berechnet werden, weil die aktuelle Standortbreite südlich von der Deklinationsbreite liegt, dann sind die Deklinationen δ und δ’ mit -1 zu multiplizieren, bevor sie in den Gleichungen Verwendung finden. Das kehrt deren Vorzeichen um und hat die Wirkung, als würde die Erdkugel auf den Kopf gestellt werden. Deswegen ist am Ende auch die mit der Gleichung 4.7 berechnete Breite mit -1 zu multiplizieren.

4.3.2 Berechnung der Länge

Die Länge wird analog dem Vorgehen in 1.4 als Chronometerlänge berechnet. Die anzuwendende Winkelberechnung nach dem Kosinus Seitensatz (Satz B.) liefert:

(4.8)  

Je nachdem, ob die Sonne am Vormittag oder am Nachmittag beobachtet worden ist, muss der berechnete Stundenwinkel zum Grt, dem Ortsstundenwinkel von Greenwich, addiert oder davon abgezogen werden.

Wir machten bisher zwei Beobachtungen, von denen die erste am Vormittag und die zweite am Nachmittag erfolgte, wie dies im Bild 4.6 gezeigt wird. Es können aber auch beide Beobachtungen am Vormittag oder beide amNachmittag stattfinden, wie es Bild 4.7 schematisch in der Mitte und rechts zeigt.

Beide Beobachtungen eignen sich dazu, die Standortlänge berechnen zu können. Wir wollen dazu die erste Beobachtung verwenden. Erfolgt diese am Vormittag, dann hat die Kulmination der Sonne am Schiffsstandort noch nicht stattgefunden. Die Sonne muss bis dahin mit ihrer konstanten Winkelgeschwindigkeit den mit der Gleichung 4.8 berechneten Stundenwinkel noch überwinden. Die Standortlänge berechnet sich somit als Summe von Grt und . Erfolgt die erste Beobachtung am Nachmittag, wie das rechts im Bild 4.7 zu sehen ist, dann ergibt sich die Länge aus dem Grt abzüglich des berechneten Stundenwinkels. Somit gilt allgemein:

(4.9)  

Die Bezeichnung λ* ist nötig, weil mit dieser Angabe eine Länge von 0° bis 360° rund um den Erdball gemeint ist. Die geografischen Längengrad-Angaben zählen jedoch vom Nullmeridian ausgehend bis 180° nach Osten und bis -180° ins Negative nach Westen. Das negative Vorzeichen bei den Längen kann entfallen, wenn stattdessen die Bezeichnung „W“ für West nachgestellt wird. Das gilt auch für Südbreiten, wenn ihnen ein „S“ nachgestellt wird.

Die Umrechnung von λ* nach λ erfolgt in zwei Schritten. Im ersten Schritt müssen Überträge behandelt werden. Die Addition oder Subtraktion von Grt und kann nämlich negative Ergebnisse hervorbringen, aber auch Werte, die größer als 360° sind. Im ersten Fall müssen 360° addiert und im zweiten Fall 360° abgezogen werden. Die nötigen Schritte zeigt das folgende Beispiel. Erster Schritt – Übertragsbehandlung:

 λ* = 363° → 363° – 360° → λ* = 3°
λ* = -15° → -15° + 360° → λ* = 345°.

Im zweiten Schritt wird zwischen Ost- und Westlängen unterschieden. Dabei gilt, dass es Westlängen sind, solange  λ* kleiner als 180° ist. Ist  λ* größer als 180°, dann ist λ* von 360° abzuziehen und es sind Ostlängen. Die Beispiele fortgesetzt ergeben schließlich:

 λ* = 3° → λ = -3° oder 3° W
λ* = 345° → λ = 360°- 345° = 15° E.

4.3.3 Realisierung als Computerprogramm

Die vorstehend beschriebene Methode lässt sich relativ einfach in ein Programm zur Standortbestimmung auf See umsetzen. Die erforderlichen Ausgangswerte sind einzig die Daten aus zwei Beobachtungen der Sonne:

• Datum und Zeit der Beobachtungen,
• beobachtete Höhen h und h’.

In den Einstellungen des Programms sollte festgelegt sein, ob die Sonne an ihrem Oberrand oder Unterrand gemessen wird. Aus der Freibordhöhe des Bootes liegt auch die Augeshöhe als Konstante fest. Der Indexfehler des verwendeten Sextanten sollte ebenfalls hinterlegt worden sein. Daraus und aus den gemessenen Höhen kann das Programm die am Sextanten abgelesenen Werte berichtigen. Das Ergebnis sind die jeweils beobachteten Höhen.
Greenwichwinkel und Deklination können entweder mit einem kleinen Modul berechnet werden, wie es z. B. am Ende von Kapitel 7 beschrieben ist oder sie werden aus einer hinterlegten Datenbank gezogen. Eingangswerte dazu sind das Datum der Beobachtung und die sekundengenauen Zeiten, in denen die Sonne im Teleskop des Sextanten auf die Kimm gesetzt worden ist.
Diese Daten sind ausreichend, um mit den Gleichungen 4.3 bis 4.7 in einem Durchgang hintereinander die Standortbreite zu berechnen. Nach der Berechnung von mittels der Gleichung 4.8 ergibt sich dann mit der Gleichung 4.9 sofort auch λ*, woraus nach ein paar Umdeutungen die geografische Länge folgt. Eine vorherige Standortschätzung ist nicht nötig und es gibt auch keine Restriktionen bezüglich einer maximal zulässigen Höhe wie es bei den Standlinienverfahren üblich ist.
Ein Problem ist vorher allerdings noch zu lösen. Damit dem Computer nicht nach jeder Beobachtung angegeben werden muss, in welcher Hemisphäre die Sonne beobachtet wurde, sollte dafür ein rechnerischer Weg gefunden werden, um herauszufinden, ob in der Gleichung 4.9 addiert oder subtrahiert werden muss.
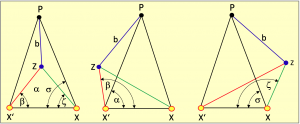
Bild 4.7 zeigt schematisch die drei möglichen Varianten, wie die Sonne von einem Standort Z aus beobachtet werden kann. Der Standort kann sich westlich oder östlich der schwarz gezeichneten Sonnenmeridiane befinden oder auch dazwischen.
Liegt er dazwischen, wie in der linken Darstellung, dann sind beide Differenzen α – β und σ – ζ positiv. In der mittleren Darstellung ist die Differenz α – β negativ und in der rechten Darstellung ist σ – ζ negativ. Daraus folgt:

1. α – β ∧ σ – ζ > 0 
erste Beobachtung Ost, 
zweite Beobachtung West.
2. α – β < 0 
beide Beobachtungen Ost,
3. σ – ζ < 0 
beide Beobachtungen West.

Mit dieser Rechenvorschrift kann ein Computerprogramm jetzt arbeiten, ohne dass die Beobachtungsrichtung jedes Mal eingegeben werden muss. Nur im Fall 3. ist die erste Beobachtung westlich und dann wird in der Gleichung 4.9 subtrahiert.

Die Winkel α und β werden normalerweise nicht gebraucht. Ihre Berechnungsgleichungen sollen aber trotzdem angegeben werden. Sie lauten:

(4.10)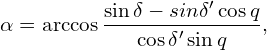  

(4.11)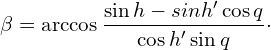  

Hier noch einmal zur Erinnerung: Zur Aufstellung dieser beiden Gleichungen muss nur die unter B. genannte Regel angewendet werden, denn alle Seiten in den Dreiecken sind bekannt.
Eine Standortberechnung mit einer Ortsveränderung zwischen den Beobachtungen mit Hilfe der Tabellenkalkulation Excel ist im Anhang 8.3 gezeigt.

 

4.4 Versegelung

Bei einer Navigation mit der Sonne muss zwischen den Beobachtungen eine angemessene Zeit verstreichen, damit die Unterschiede zwischen den Sonnenständen groß genug sind und sich die Höhenkreise in einem genügend großen Winkel (möglichst >30°) kreuzen. Da in der Zwischenzeit weitergesegelt wird, verändert sich der Schiffsort. Wenn die während der ersten Beobachtung festgestellte Höhe der Sonne auf den Ort der zweiten Beobachtung hochgerechnet werden kann, dann hat man zum Zeitpunkt der zweiten Beobachtung gleichzeitig zwei Gestirne, eine eingebildete Sonne an der Position, in der sie während der ersten Beobachtung stand, und die wahre Sonne. Damit kann dann ein Standort auf dieselbe Weise berechnet werden, als würde man zwei Sterne zur selben Zeit oder unmittelbar nacheinander beobachtet haben.
Diese Aufgabe gilt für alle Navigationsmethoden, bei denen nur mit einem Gestirn navigiert wird, bei Sumner und Hilaire ebenso wie bei Gauß. Die jeweils erfolgte Ortsveränderung zwischen den Beobachtungen, bestehend aus einer Distanz über Grund und einem gefahrenen Kurs über Grund, muss in diesen Fällen mithilfe einer Koppelnavigation (engl. Dead Reckoning) festgestellt werden.

4.4.1 Versegelung nach Douwes

Wir nehmen einmal an, dass sich die Position eines Gestirns an der Himmelskugel nach einer Beobachtung nicht mehr verändert. Das Gestirn würde damit einen geostationären Zustand beibehalten und somit bliebe auch die Position seines Bildpunktes auf der Erdoberfläche unverändert. Verändern wir daraufhin unseren Standort, weil wir nach der Beobachtung weitersegeln, dann würde sich unsere Entfernung zum Bildpunkt ändern, größer oder kleiner werden. Diese Entfernung ist der Radius des Höhenkreises des geostationären Objektes, auf dem wir uns stets befinden.
Am Ort der zweiten Beobachtung wollen wir unsere Position feststellen, indem wir dazu die Höhen der wahren Sonne und der fiktiven geostationären Sonne benutzen. Das geht aber nur, wenn wir die Höhe der fiktiven Sonne, deren Position unverändert geblieben ist, aus der inzwischen versegelten Distanz und dem versegelten Kurs, jeweils über Grund, berechnen können.

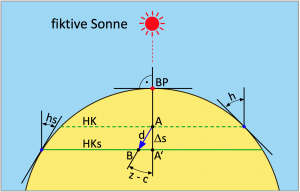
Bild 4.8 visualisiert den Vorgang als Grafik. Nach einer ersten Beobachtung der Sonne, wobei deren Höhe mit h gemessen wurde, bleibt diese als fiktive geostationäre Sonne in ihrer Position und damit auch ihr Bildpunkt BP auf der Erdoberfläche fix. Jetzt wird aber weitergesegelt und zwar wird die Strecke von A nach B in einem Kurs von c zurückgelegt. Dadurch ändert sich die Höhe der fiktiven Sonne von h nach hs und damit der Radius des Höhenkreises um Δs.
Eine positive Änderung des Zenitabstandes ist gleich einer negativen Höhenänderung Δs = -Δh). Zur Berechnung dieser Höhenänderung hat Douwes eine Formel angegeben. Wir wollen diese jetzt nicht herleiten, sondern lediglich anführen:

   

Hierin bedeuten d die zurückgelegte Distanz über Grund (DMG = Distance Made Good) in nautischen Meilen und c ist der dabei gefahrene mittlere Kurs bzw. Kurs über Grund (CMG = Course Made Good). Weil die Höhenänderung genau wie auch die Höhe in Grad angegeben sein muss, ist eine Division durch 60 NM/Grad erforderlich. Der Buchstabe z ist dabei das Azimut. 
Die Höhe der fiktiven Sonne nach der Versegelung errechnet sich damit einfach als

(4.12)  

Dieser Vorgang wird Höhenanpassung nach einer Versegelung genannt.
Die in dieser Formel benötigten Daten von d und c sind Ergebnisse einer Koppelnavigation, die entweder „zu Fuß“ oder mithilfe eines kleinen Programms erfolgen kann. Das Azimut z ist vergleichbar mit einem rechtweisenden Kurs auf den Bildpunkt. Rechtweisend bedeutet, dass der Winkel z ab dem nach Norden weisenden Meridian p bzw. p’ zu messen ist. Wir wollen jetzt das Azimut berechnen.
Im Bild 4.9 besteht das Azimut zur Sonne X als Winkel zwischen den Dreieckseiten b und s und das Azimut zur Sonne X’ als Winkel zwischen b und s’. Der Innenwinkel z* dieser Dreiecke wird mit dem Kosinus Seitensatz gemäß Regel 2 auf Seite 81 berechnet. Die allgemeine Formel auf die jeweils gemessene Höhe angewendet lautet:

(4.12)  

Da der Arkuskosinus nur Winkel zwischen 0° und 180° Grad liefern kann (Innenwinkel), das Azimut aber von 0° bis 360° reicht, müssen Azimute, die sich nach dem Schiffsmittag ergeben, wenn also die Sonne den Schiffsort überholt hat und dadurch der LHA erneut von 0° an zu zählen beginnt, nach folgenden Regeln betrachtet und eventuell korrigiert werden:

   

   

Wenn der LHA 180° besitzt, dann befindet sich der Bildpunkt der Sonne auf der gegenüberliegenden Seite der Erde und es ist tiefste Nacht. Vom Schiffsmittag an bis dahin war er immer kleiner als 180°. In dem Fall ist das Azimut der Außenwinkel wie es Bild 4.9 rechts zeigt.

Von Mitternacht an bis zum Schiffsmittag wächst der LHA dann von 180° auf 360°, ist also stets größer als 180°. In dem Fall kann nur der Innwinkel des im Bild 4.9 links gezeigten Polardreiecks als Azimut berechnet werden und z = z*.
In der Zeit, als es noch keine Rechenmaschinen gab, wäre eine analytische Berücksichtigung einer Versegelung gar nicht erst in Frage gekommen. Wie die beiden vorstehenden Formeln zeigen, braucht man zur Berechnung des Azimuts die Standortbreite und den LHA, der nur über die Standortlänge erhalten wird. Das bedeutet nicht weniger, als dass der Standort am Ort der zweiten Beobachtung einmal komplett auszurechnen ist, ohne dass dabei eine Versegelung betrachtet wird. Mit Logarithmen hätte das ein schneller menschlicher Rechner vielleicht in ein bis zwei Stunden geschafft. Dabei ist noch keine Versegelung berücksichtigt. Das Ergebnis wäre nur ein nahe gelegener Standort, der weder der aktuelle Standort ist noch der Ort der ersten Beobachtung. Doch erst dieser fiktive Standort ermöglicht eine sehr gut angenäherte Berechnung des LHA und auch des Azimuts. Zwischenzeitlich müsste auch noch eine Koppelrechnung vorgenommen werden, um Distanz und Kurs der Versegelung herauszubekommen.
Doch dann würde der zweite Akt folgen, in dem die im Abschnitt 4.3.1 ab 3) verwendeten Formeln zur Berechnung der versegelten Breite und die im Anschluss folgenden Formeln zur Längenberechnung noch einmal durchgerechnet werden müssten. Bei diesem zweiten Durchgang wird anstelle von h die angepasste Höhe hs aus Gleichung 4.12 verwendet. Mehr Rechenstress mit Logarithmen ist eigentlich kaum vorstellbar – und das für eine einzige mathematisch exakte Standortbestimmung. Daher verwundert es auch nicht, dass im 19. Jahrhundert zu Näherungslösungen gegriffen wurde.

4.5 Standort aus der Mittagsbreite

Bei allen Methoden, die nur mit der Sonne arbeiten, gibt es Schwierigkeiten, aus einer Höhe, die am oder in der Nähe des Schiffsmittags gemessen wird, einen Standort zu errechnen. Eines der beiden Dreiecke im Bild 4.5, entweder XPZ oder X’PZ, mutiert am Mittag zu einer senkrechten Linie, weil dann alle Seiten des Dreiecks mit dem Sonnenmeridian zusammenfallen. So kann ein Standort nur noch aus der Mittagsbreite und einer Höhengleiche hergeleitet werden. Dies kann in manchen Situationen sogar einige Vorteile bieten, wenn nämlich in der Nähe der Deklinationsbreite oder sehr weit im Norden oder Süden gesegelt wird und die Höhenkreise an diesen Orten entweder sehr klein oder sehr groß sind.
Die Mittagsbreite wird bekanntlich dadurch bestimmt, dass die Kulminationshöhe der Sonne gemessen wird. Je nachdem, ob die Sonne im Süden oder Norden peilt, werden Zenitabstand und Deklination addiert oder die Deklination vom Zenitabstand subtrahiert. Im Einzelnen gilt für die Mittagsbreite:

(4.14)  

(4.15)  

Beim Kombinieren der Navigation mit Höhenkreisen und der Mittagsbreite gibt es zwei Varianten, die nachfolgend untersucht werden.

4.5.1 Höhenkreis zuerst

Bei dieser Variante wird am Vormittag die Sonne in der östlichen Hemisphäre beobachtet, wie es die Grafik im Bild 4.10 zeigt. Der Kimmabstand wird mit h gemessen und ist mit s = 90° – h der Radius des im Bild gestrichelt dargestellten noch nicht versegelten Höhenkreises. Die Beobachtungszeit liefert über einen Almanach die Sonnenpositionen Grt und δ.
Einige Zeit später, am Schiffsmittag, wird die Kulmination der Sonne festgestellt und daraus die Mittagsbreite _M berechnet. Es sollte möglichst vorher schon ermittelt werden, wann Schiffsmittag ist. Das geht am elegantesten mit der in Kapitel 2 beschriebenen App. Diese zeigt die Zeit des Schiffsmittags immer nach einer zweiten Beobachtung an. Diese zweite Beobachtung kann schon eine Stunde nach der ersten Beobachtung, aber noch am Vormittag gemacht werden.
Am Schiffsmittag befindet sich der eigene Standort Z auf dem kleinstmöglichen Höhenkreis, der im Bild als roter Kreis dargestellt ist. Aus der gemessenen Kulminationshöhe kann jedoch kein Standort hergeleitet werden. Das Polardreieck X’ZP existiert nicht mehr, es ist zu einer Linie geworden. Unter Verwendung von δ’ kann jedoch die Mittagsbreite M bestimmt werden. Sie ist in diesem Fall auch gleich die Standortbreite:

   

Seit der ersten Beobachtung wurde jedoch eine Distanz d auf einem Kurs c zurückgelegt. Dadurch hat sich der Durchmesser bzw. Radius des gestrichelt gezeichneten Höhenkreises geändert. Die Höhenanpassung wird hier nach Douwes berechnet.

Das dazu gebrauchte Azimut folgt aus M, δ und h. Da die Messung vormittags gemacht wurde, ist das berechnete Azimut z* auch das wahre Azimut und die angepasste Höhe hs kann unter Verwendung der Versegelungskomponenten d und c berechnet werden.
Tatsächlich hätte das Azimut für den Standort der ersten Beobachtung berechnet werden müssen. Dies war allerdings nicht möglich, da zu dem Zeitpunkt noch keine Breite bekannt gewesen ist. Angesichts der großen Entfernung zum Bildpunkt der Sonne ist ein dadurch entstehender Rechenfehler, weil die Mittagsbreite eingesetzt wird, ohne Weiteres vernachlässigbar – ebenso wie die Tatsache, dass die Höhenanpassungsformel auf Regeln der ebenen Trigonometrie beruht. Auch das ist bei den geringen Strecken, die eine Versegelung ausmachen, ohne große Bedeutung. Sehr viel mehr Abweichungen entstehen dadurch, dass die während einer Versegelung gefahrenen Schläge nicht exakt genug eingeschätzt und zusammengerechnet werden.
Der durch die angepasste Höhe hs entstandene Zenitabstand beträgt jetzt ss und ist der Radius des im Bild grün dargestellten Höhenkreises. Aus der mit Gleichung 4.12 angepassten Höhe hs, der Deklination δ’ und der Mittagsbreite als drittes Element sind nun alle Seiten des Polardreiecks XPZ als Komplemente bekannt und der Winkel ist bestimmbar. Daraus ergibt sich dann die Standortlänge λ* als Summe von und Grt:

(4.16)  

(4.17)  

Auch hier müssen zunächst eventuelle Überträge entfernt werden. Wenn danach λ* zwischen 0° und 180° liegt, dann handelt es sich um Westlängen. Werte, die größer als 180° sind, müssen von 360° subtrahiert werden und sind dann Ostlängen.

4.5.2 Mittagsbreite zuerst

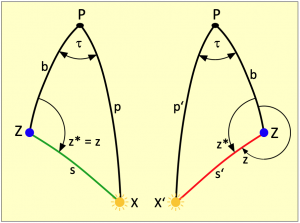
Für den Fall, dass die Mittagsbreite zuerst bestimmt wird, kann sich diese durch Versegeln ändern. Zum Zeitpunkt der Messung eines Nachmittags-Höhenkreises beträgt sie dann

   

und es ist die versegelte Standortbreite. Hierin ist Δ die Breitenkomponente der Versegelung. Der Betrag von Δ ist negativ, wenn die Ortsveränderung einen stärkeren südlichen Anteil hatte, die Breite sich also verringert hat, und positiv, wenn die Breite im Zuge der Versegelung zugenommen hat.

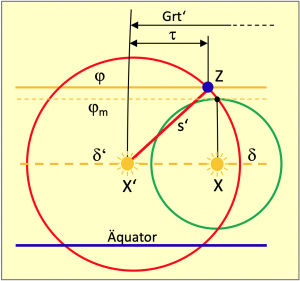
Bild 4.11 zeigt ein Beispiel für eine Versegelung der Mittagsbreite in nördliche Richtung, was daran zu erkennen ist, dass der Standort nach Versegelung nördlicher liegt als die Mittagsbreite. Nach Messung der Kulmination der Sonne X am Schiffsmittag muss der Greenwichwinkel nicht bestimmt werden. Es genügt die Feststellung der Deklination mithilfe eines Almanachs, damit daraus die Mittagsbreite berechnet werden kann. Da die Sonne im Süden beobachtet wurde, ergibt sich die Mittagsbreite einfach als 90° – h + δ.
Zum Zeitpunkt der zweiten Beobachtung am Nachmittag wird die wahre Sonne X’ in einer Höhe von h’ beobachtet. Nach der Entnahme der Deklination δ’ für diesen Zeitpunkt aus dem Almanach sind alle drei Seiten des Polardreiecks bzw. ihre Komplemente bekannt. Wir sind also in der Lage, den Stundenwinkel zu berechnen. Da wir auch gleich den Greenwichwinkel Grt aus dem Almanach herausgelesen haben, kann jetzt ebenfalls die Länge λ* ermittelt werden. Die Formeln dafür lauten:

(4.18)  

(4.19)  

Zum Schluss muss die erdumlaufende Länge λ* dann noch auf die geografische Nord- oder Südlänge umgewandelt werden.

 

4.6 Die Methode von Carl Friedrich Gauß

Johann Carl Friedrich Gauß war ein deutscher Mathematiker, Statistiker, Astronom, Geodät, Physiker und Elektrotechniker. Wegen seiner überragenden wissenschaftlichen Leistungen galt er bereits zu seinen Lebzeiten als „Princeps mathematicorum“. Gauß leitete in den Jahren 1821 – 1825 die Vermessung des Königreiches Hannover. Doch sein Interesse an der Landvermessung hatte er schon viel früher unter Beweis gestellt.
Zwischen 1802 und 1807 führte er trigonometrische Vermessungen unter anderem weit über das Stadtgebiet von Braunschweig hinweg aus.
Dabei benutzte er einen Sextanten, den er sich von seinem Freund Franz Xaver von Zach auslieh. Unter Anwendung der von ihm selbst entwickelten Methode der kleinsten Quadrate konnte er Beobachtungsfehler minimieren und auf diese Weise sehr präzise Messungen anstellen.
Im Jahre 1807 wurde Gauß zum Universitätsprofessor und Sternwarten-Direktor in Göttingen berufen. Die Sternwarte wurde allerdings erst 1816 fertiggestellt. Neben der Mathematik und seinen Landesvermessungen war auch die Astronomie ein Gebiet, auf dem Gauß mit bemerkenswerten Leistungen internationales Ansehen genoss.

Gauß war zwar kein Seemann, doch eine Ortsbestimmung auf See unterscheidet sich nicht wirklich von einer Ortsbestimmung an Land. Schließlich muss auch ein Kartograf Längen- und Breitengrade auf seinen Landkarten einzeichnen können. So war die Dissertation eines Herrn Kraft für Gauß der Anlass zu einer bemerkenswerten Arbeit, mit der er gleichzeitig auch eine Lösung des Zweihöhenproblems der Seefahrer lieferte. In seiner Arbeit beschreibt W. Kraft, wie aus der gemessenen Höhe zweier Sterne die geografische Breite berechnet wird.
Seine Arbeit basierte auf dem damals jedem Astronomen bekannten Modell mit den zwei geläufigen Sternpositionen X und X’, dem zu bestimmenden Scheitelpunkt Z und dem Nordpol P, wie es Bild 4.13 zeigt. Doch erstmalig gab es einen entscheidenden Unterschied. Herr Kraft stützte sich nicht auf das grafische Modell, sondern auf ein Gleichungssystem, in das er die Zeichnung zuvor verwandelt hatte und diese damit mathematisch exakt mit zwei verbundenen Gleichungen beschrieb. Diese Transformation von einem allgemein verständlichen bildhaften Modell in ein abstraktes mathematisches Modell war ein neuer Ansatz.
Anhand einer gezeichneten Sache entsteht ein visueller Kontakt mit einem Problem, das sich leichter vorgestellt werden kann. An einem gezeichneten Modell ist es einfacher, Lösungswege zur Berechnung noch unbekannter Elemente aus vorhandenen bekannten Elementen zu entwickeln. So kann man Schritt für Schritt echte Elemente oder Teile eines solchen Modells berechnen und dabei verschiedene Lösungswege ausprobieren, bis man auf eine gewünschte oder annehmbare Lösung kommt. Das ist die Arbeitsweise eines Ingenieurs.
Herr Kraft war aber kein Ingenieur, sondern Mathematiker und hat deshalb die Bildsprache, die eine Zeichnung vermittelt, in seine abstrakte mathematische Sprache übersetzt. Er stellte für die beiden Dreiecke XPZ und X’PZ je eine Gleichung auf. In beiden Gleichungen sind die Breite und der Stundenwinkel als Unbekannte enthalten. Damit liegt ein Gleichungssystem mit zwei Unbekannten vor. Sein Ziel bestand wohl darin, mit einer Auflösung den Rechenweg, der mit den Gleichungen 4.3 bis 4.7 gegeben war, abzukürzen. Das Gleichungssystem lautet:

   

   

Diese beiden Gleichungen und Bild 4.13 sind also absolut identisch und wechselseitig ineinander überführbar. Der Unterschied ist nur, wie bereits erwähnt, dass das gezeichnete Bild der Sprache des Praktikers entspricht und das Gleichungssystem der des Mathematikers.
Die Gleichungen, es ist Anwendung des Kosinus Seitensatzes, enthalten die transzendenten Funktionen Sinus und Kosinus. Doch dafür gibt es keinen allgemeinen Lösungsweg, der hätte angewendet werden können. Tranzendente Gleichungssysteme gelten gemeinhin sogar als unlösbar.
Herrn Kraft ist es zwar gelungen, beides, die Breite und den Stundenwinkel zu berechnen, jedoch in einer äußerst verwickelten Auflösung. Gauß bemerkte dazu, dass es stattdessen einfacher wäre, die Breite durch eine direkte Betrachtung dreier Dreiecke zu finden. Das ist der Rechenweg mit den Gleichungen 4.3 bis 4.7. Außerdem fand er die spezielle Einschränkung des Herrn Kraft sonderbar, dass die Höhen der beiden Sterne zum selben Zeitpunkt gemessen werden müssten.
Das hätte zwei Messwerkzeuge und zwei Beobachter gleichzeitig erfordert. Die Sonne würde dann als Navigationsgestirn sogar ausscheiden, weil sie zur selben Zeit nur eine Höhe besitzen kann. Gerade der Sonne maß Gauß eine besondere Bedeutung zu, denn sie scheint den ganzen Tag und der Winkel am Sextanten ist bei Tageslicht viel besser abzulesen.

Gauß erkannte den Vorteil, den dieser neue mathematische Ansatz für die Arbeit in der Kartografie und für die Seefahrer bedeuten könnte. So machte er sich daran, mit dem Ansatz des Herrn Kraft einen eigenen und besseren Lösungsweg zu erarbeiten. Das Ergebnis seiner Arbeit, die er schon 1808 anfertigte, erschien in „Bodes Astronomischem Jahrbuch“ für das Jahr 1812 unter dem Titel:

„Neue Methode, aus der Höhe zweier Sterne die Zeit und die Polhöhe zu bestimmen, nebst astr. Beobachtungen, vom Herrn Professor Gauß in Göttingen.“

Ein Ausschnitt dieses Aufsatzes ist im Beitrag 8 wiedergegeben. Es hätte eine Sternstunde in der Hochseenavigation sein können und Gauß selbst war davon überzeugt, eine Methode gefunden zu haben, die für praktische Anwendungen endlich geeignet sei, doch er sollte sich irren.
Tatsächlich ermöglichte sein Formelapparat eine präzise Berechnung des Breitengrades und der Zeit. Die Berechnung mit Logarithmen war gegenüber der Methode mit den Polardreiecken etwa um ein Drittel verkürzt. Die Berechnung der Zeit ermöglichte außerdem eine Längenbestimmung.
Doch das war nicht das Problem. Seine Auflösung bestand letztlich nur aus Substitutionen, die er mit F, V, W und G bezeichnete, die jedoch keinem einzigen Element aus der Praxis oder dem bekannten Grafikmodell im Bild 4.13 oder 4.5 zugeordnet werden konnten. Zwar war es möglich, mit diesen Substitutionen Breite und Zeit sowie schließlich aus der Zeit die Länge ganz einfach zu errechnen, doch niemand konnte daraus eine Vorstellung entwickeln, was das alles genau ist. Für Praktiker war weder der Weg der Analyse nachvollziehbar noch hatten die Ergebnisse einen Wiedererkennungswert. 
Gauß fand einen Lösungsweg, ohne sich um eine einzige Formel aus der sphärischen Trigonometrie zu bemühen, die für die damaligen Seeleute gerade eine neue Herausforderung war. Er fand eine Auflösung allein durch die Anwendung einer mathematischen Analyse. Damit war seine Methode nicht vermittelbar und das gilt noch immer. Sie ist in der nautischen Literatur nicht überliefert und heute völlig unbekannt. Ich möchte die Formeln an dieser Stelle auch nicht herleiten, sondern nur vorstellen und darauf eingehen, wie sie benutzt werden. Ihre Herleitung ist Teil des Anhangs. Der Formelapparat besteht aus sieben recht übersichtlichen Gleichungen:

(4.20)  

(4.21)  

(4.22)  

(4.23)  

(4.24)  

(4.25)  

(4.26)  

Obwohl sich die Formeln nicht verständlich erklären lassen, wie z. B. beim Kosinus Seitensatz mit Dreieckseiten und davon eingeschlossenen Winkeln, kann man doch sehr gut damit rechnen. So liefert der Kosinus infolge seiner Symmetrie (siehe Bild 4.3) stets zwei Ergebnisse, ein positives und ein negatives. Das betrifft hier die Gleichung 4.22 zur Berechnung von W. Daraus errechnen sich dann auch zwei mögliche Standorte, die Bild 4.13 mit Z und Y nördlich oder südlich der Deklinationsbreite aufzeigt. Mit dem Faktor P in der Gleichung 4.22 kann somit einfach vorgegeben werden, welcher Standort auszurechnen ist. Mit P = 1 ist es der nördliche Schnittpunkt Z der Höhenkreise und mit P = -1 der südliche Schnittpunkt Y.

Bemerkenswert dürfte auch die Gleichung 4.24 sein. Dieses , das hier über den Arkustangens ausgegeben wird, ist eine Längenkomponente, die automatisch die Peilrichtung berücksichtigt. Diese muss deshalb nicht mehr angegeben werden, wie das im Abschnitt 4.3.2 beschrieben worden ist. Eine programmtechnischen Realisierung kommt also ohne die Gleichungen 4.10 und 4.11 aus. Die Länge wird einfach nur als Summe von gemäß Gleichung 4.24 und Grt berechnet. Außerdem entfällt die Multiplikation der Deklinationen mit -1, wenn der südliche Schnittpunkt berechnet werden soll, wie das bei der geometrisch basierten Lösungsfindung in 4.3.1 der Fall ist.
Auch wenn die Tageszeit einer zweiten Beobachtung kleiner als die einer ersten Beobachtung ist, weil z. B. beim Segeln im pazifischen Raum ein Datumswechsel erfolgte, wird das von den Gauß Formeln berücksichtigt. Alles in allem ist der Formelapparat sehr kompakt und ideal zur Benutzung in einem Computerprogramm geeignet.
Nachdem in ein derartiges Programm Kimmabstände und Zeiten von zwei Beobachtungen der Sonne eingegeben worden sind, kann die Berechnung starten. Außerdem stehen zum Zeitpunkt der zweiten Beobachtung die Versegelungsdaten Distance d und Course c bereits zur Verfügung. Der Algorithmus läuft dann folgendermaßen ab:

1. Aus beiden Beobachtungszeiten berechnet das Programm Greenwichwinkel und Deklinationen. Alternativ können diese auch aus einer Datenbank gezogen werden.
2. In einem Zug hintereinander werden alle Gleichungen von 4.20 bis 4.26 ausgerechnet. Falls in der Zeit zwischen den Beobachtungen eine Ortsveränderung erfolgte, bezeichnen die Koordinaten und λ* einen unbekannten Ort in der Nähe, der nach einer Bestimmung von LHA zur Berechnung des Azimuts z für eine Höhenanpassung gebraucht wird.
3. Der Ortsstundenwinkel LHA wird aus λ* und Grt berechnet, um daraus das Azimut z nach Gleichung 4.13 bestimmen zu können.
4. Mit dem Azimut sowie den Daten von versegelter Distanz und abgesetztem Kurs ist jetzt die angepasste bzw. versegelte Höhe hs gemäß Gleichung 4.12 zu berechnen.
5. Mit der angepassten Höhe hs wird ab Gleichung 4.22 erneut in die Berechnung eingestiegen und alle Formeln bis einschließlich Gleichung 4.26 werden erneut durchlaufen, wobei jetzt hs anstelle von h verwendet werden muss.

Damit steht der versegelte Standort mit der Länge λs* und der Breite s fest (Index s = sailed). Es fehlt noch die Umstellung von λs* auf den geografischen Längengrad entsprechend der üblichen Deutung, dass λs* bis 180° Westgrade angibt und darüber hinausgehende Werte, von 360° subtrahiert, Ostgrade sind.

Die Gauß Formeln sind allerdings nur dann ganz problemfrei, wenn die Höhenkreise am Äquator gespiegelt sind, wie an den Tagundnachtgleichen. Zu allen anderen Zeiten liegen die Meridiane entweder im Nordhalbkreis oder im Südhalbkreis enger zusammen, mit der Folge von Berechnungsausfällen bei sehr kleinen Sonnenhöhen oder zu spitzen Schnittwinkeln zwischen den Höhenkreisen. Hier wäre dann nachzuhelfen. Wird die Differenz F – δ negativ, dann muss V um π bzw. 180° vermehrt werden. Gleiches gilt für τ das um π bzw. 180° zu vermehren ist, wenn das Produkt von P ･(G – δ) negativ wird. Letztlich ist dann noch das Produkt P･(π/2 + W – V) zu prüfen. Ist es negativ, dann wird G bei positiven Deklinationen um π bzw. 180° vermindert und bei positiven Deklinationen um denselben Betrag vermehrt.

(näheres dazu am Ende von Kapitel 8 unter „Was noch zu sagen ist“)

---

Einige Autoren ordnen C. F. Gauß fälschlicherweise die unter 4.3 beschriebene Methode zu. Genau diesen Lösungsweg wollte Gauß aber gerade vermeiden. Nachdem er in seiner Publikation das im Bild 4.13 dargestellte geometrische Modell verbal beschrieben hatte, formulierte er als Einleitung zu seinem Rechenweg den folgenden Satz:

„Dieses alles beruhet auf rein geometrischen, freilich ganz einfachen Betrachtungen: es wird aber ohne Zweifel manchem angenehm seyn, eine directe Auflösung dieses Problems auf blos analytischem Wege entwickelt zu sehen wodurch sich aufs Neue bestätigen wird, daß alle Wahrheiten, welche aus geometrischen Betrachtungen abgeleitet werden, ebenso zierlich mit Hülfe der Analyse entdeckt werden können, wenn diese nur auf die rechte Art behandelt wird.“

Gauß suchte also eine rein mathematische Lösung unter Vermeidung geometrischer Betrachtungen über Dreiecke, Seiten, Winkel und sphärischer Trigonometrie und hoffte, dass diese einfacher ist, als die bisher bekannte.
Der wahre von Gauß gefundene Lösungsweg ist in der nautischen Literatur nie wieder in Erscheinung getreten und kann auch in der internationalen Literatur nirgendwo gefunden werden, was äußerst schade ist, denn für eine Digitalisierung der Astronavigation sind gerade solche Lösungen von Bedeutung. Deshalb habe ich einen längeren Auszug aus seiner Originalveröffentlichung von 1809 der Anlage beigefügt. Diese Wiedergabe dürfte ein Leckerbissen für alle Mathematikfans sein.

 

4.7 Beispiel einer algebraischen Standortberechnung

Im folgenden Beispiel wird eine Berechnungstabelle gezeigt, wie sie in einer Tabellenkalkulation wie z. B. Excel oder Numbers verwendet werden kann und die eine komplette Positionsberechnung nach zwei Sonnenbeobachtungen mit Versegelung zeigt. Grundlage der Berechnungen sind die in den Abschnitten 4.3 und 4.4 gemachten Ausführungen.

1. Datum                                12. Mai 2023
2. erste Beobachtung           oz = 9:01:18 UTC;      beobachtete Höhe:     h = 38° 15,15′
3.  zweite Beobachtung      oz_ = 11:34:41 UTC;     beobachtete Höhe:    h_ = 65° 23,66′
4. Versegelung                     (distanze made good) dmg = 19 NM; (course made good) cmg = 135°

Die beobachteten Höhen h und h_ ergeben sich nach der jeweiligen Beschickung der Sextantenablesungen.

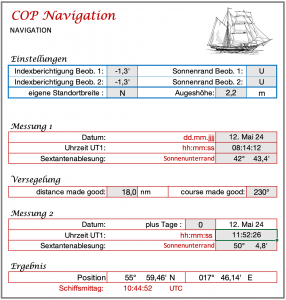
Die Beobachtungszeiten, bestehend aus Datum und Tageszeiten liefern die Deklinationen und die Greenwich Ortsstundenwinkel und Grt. Dazu ist ein Nautical Almanac erforderlich. Alternativ können diese Ephemeriden auch durch Berechnung gefunden werden, wie das im Kapitel 7 4.4 beschrieben wird. Konkret ergeben sich nach Berechnung die folgenden Daten:

•  d = 18,111° = 0,3161_rad           grt = 316,232° = 5,5193_rad
• d_ = 18,137° = 0,3166_rad         grt_ = 354,478° = 6,1886_rad

Die Polkonstante P = 1 oder -1, mit der festgelegt wird, ob der nördlich gelegene oder der südlich gelegene Schnittpunkt der sich überlappenden Höhenkreise berechnet werden soll, ergibt sich aus der eigenen Position und aus der Frage, ob diese nördlich oder südlich der Deklinationsbreite liegt. Die Tafel 4.2 enthält in der Namensspalte die in Excel einzutragenden Namen, die zusätzlich zu den Namen h und h_ für die beiden Beobachtungen und d bzw. d_ und grt bzw. grt_  für die Ephemeriden der Beobachtungen eingetragen werden müssen. Sobald eine Zelle mit dem Bogenmaß (Radiant) eines Wertes angeklickt wird, erscheint ganz oben links im Excel Arbeitsblatt dann der zugehörige Name. Die folgende Tafel 4.2 enthält dazu alle Werte. Die Grad-Spalte errechnet sich aus der radiant-Spalte mit jeweils der Formel =GRAD(x_rad).

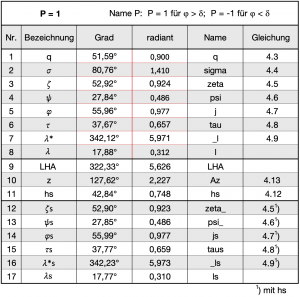
Die Tafel berechnet in den Zeilen 1 bis 8 einen Bezugsstandort (ähnlich einem Gissort), der für die Einbeziehung der Versegelung wichtig ist. In den Zeilen 9 bis 11 wird die Höhenanpassung infolge der Versegelung berechnet und in den Zeilen 12 bis 17 schließlich die Position nach Versegelung. Diese ergibt sich aus = -11,075° und = 37,849° als:

38° 5,33′ N / 011° 4,47′ W

Die letzte Tafel enthält die dazu in der radiant-Spalte einzusetzenden Formeln in Excel-Schreibweise, die einzeln per drag and drop in ein Excel Arbeitsblatt kopiert werden können. (Das vorangestellte Leerzeichen muss entfernt werden, damit Excel mit der Formel rechnen kann.)

Nr.	Bezeich- nung	Gleichungen in der Spalte radiant in Excelschreibweise
1	q	=ARCCOS(SIN(P*d)*SIN(P*d_)+COS(P*d)*COS(P*d_)*COS(grt_-grt))
2	q	=ARCCOS((SIN(P*d_)-SIN(P*d)*COS(q))/(COS(P*d)*SIN(q)))
3		=ARCCOS((SIN(h_)-SIN(h)*COS(q))/(COS(h)*SIN(q)))
4		=sigma-zeta
5		=ARCCOS((SIN(h)-SIN(P*d)*SIN(j))/(COS(P*d)*COS(j)))
6		=P*(ARCSIN(SIN(h)*SIN(P*d)+COS(h)*COS(P*d)*COS(psi)))
7		=grt+WENN(psi>0;1;-1)*tau
8		=WENN(_l<PI();-_l;2*PI()-_l)
9	LHA	=WENN(grt+l<0;grt+l+2*PI();WENN((grt+l)>2*PI();grt_+l-2*PI();grt+l))
10	z	=WENN(LHA>PI();ARCCOS((SIN(d)-SIN(h)*SIN(j))/(COS(h)*COS(j)));(2*PI()-ARCCOS((SIN(d)-SIN(h)*SIN(j))/(COS(h)*COS(j)))))
11	hs	=BOGENMASS(dmg/60)*COS(Az-BOGENMASS(cmg))+h
12		=ARCCOS((SIN(h_)-SIN(hs)*COS(q))/(COS(hs)*SIN(q)))
13		=sigma-zeta_
14		=P*(ARCSIN(SIN(hs)*SIN(P*d)+COS(hs)*COS(P*d)*COS(psi_)))
15		=ARCCOS((SIN(hs)-SIN(P*d)*SIN(js))/COS(P*d)/COS(js))
16		=grt+WENN(psi_>0;1;-1)*taus
17		=WENN(_ls<PI();-_ls;2*PI()-_ls)

Tafel 4.3: Berechnungsformeln

Ein fertiges Excel Arbeitsblatt, mit dem ein Standort nach der Methode von Carl Friedrich Gauß berechnet werden kann, wie das hier im Kapitel 4.6 beschrieben ist, kann unter

gaussmethode

heruntergeladen werden.